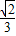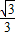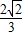题目内容
已知正三棱锥D-ABC的外接球的球心O满足| OA |
| OB |
| CO |
分析:由题意球的三角形ABC的位置,以及形状,利用球的体积,求出球的半径,求出棱锥的底面边长,求出棱锥的体积即可.
解答:解:正三棱锥D-ABC的外接球的球心O满足
+
=
,
说明三角形ABC在球O的大圆上,并且为正三角形,球的体积为16π.
球的半径为:R=
,棱锥的底面正三角形的高为:
底面三角形的边长为:
正三棱锥的体积为:
×
×(
)2×
=3
故答案为:3
| OA |
| OB |
| CO |
说明三角形ABC在球O的大圆上,并且为正三角形,球的体积为16π.
球的半径为:R=
| 3 | 12 |
3
| |||
| 2 |
底面三角形的边长为:
3
| |||
|
正三棱锥的体积为:
| 1 |
| 3 |
| ||
| 4 |
3
| |||
|
| 3 | 12 |
| 3 |
故答案为:3
| 3 |
点评:本题考查球的内接体问题,球的体积,棱锥的体积,考查空间想象能力,转化思想,计算能力,是中档题.

练习册系列答案
相关题目