题目内容
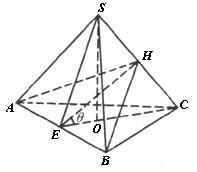
已知正三棱锥S-ABC中，高SO==3，底面边长为
，过棱AB作截面ABD交侧棱SC于点D，截面与底面所成二面角为
q，当
q为何值时，SC与平面ABD垂直？
答案：
解析：
解析：
| 解：设CO交AB于E，则可得CE^AB，连DE，由三垂线定理得DE^AB，
∴ ÐDEC为二面角D-AB-C的平面角，即ÐDEC==
|
q，∵ SC^AB，欲使SC^平面ABD，只要SC^DE，∵ SO^EC，∴ ÐOSC==ÐDEC=q．在ÐABC中，
．在Rt
SCO中，
，即tan
=
，∴ 当
=arctan
时，SC与平面ABD垂直．
练习册系列答案
相关题目
