Question

（09年长沙一中一模理）（13分）已知椭圆C的中心为坐标原点O，焦点F₁，F₂在x轴上，离心率为，点Q在椭圆C上且满足条件：= 2， 2．

（Ⅰ）求椭圆C的方程；

     （Ⅱ）设A、B为椭圆上不同的两点，且满足OA⊥OB，若(∈R)且，试问：是否为定值．若为定值，请求出；若不为定值，请说明理由。

Answer 1

解析：（Ⅰ）设椭圆方程为，∵e =，∴a = 2c

∴，．

又2      ∴cos∠F₁QF₂ =．

由|F₁F₂|² = |QF₁|² + |QF₂|² 2|QF|?|QF₂|cos∠F₁QF₂得a = 2，c = 1，b² = 3

∴椭圆C的方程为．          ……5分

（Ⅱ）依题意可知，点M为由点O向直线AB所作的垂线的垂足．

设A(x₁，y₁)，B(x₂，y₂)

（1）当x₁ = x₂时，直线OA、OB的斜率分别为±1，解方程组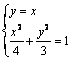得x =±．

∴．                       ……6分

（2）当x₁≠x₂时，设AB的直线方程为：y = kx + m，代入得

(3 + 4k²)x² + 8mkx + 4m² 12 = 0

x₁ + x₂ =，x₁?x₂ =          ……8分

∵，∴=

∴7m² = 12 (k² + 1)     ∴      ……11分

又∵．

综上所述．                 ……13分