题目内容
在平面直角坐标系中,已知点 ,点
,点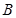 在直线
在直线 :
: 上运动,过点
上运动,过点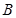 与
与 垂直的直线和线段
垂直的直线和线段 的垂直平分线相交于点
的垂直平分线相交于点 .
.
(1)求动点 的轨迹
的轨迹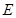 的方程;
的方程;
(2)过(1)中的轨迹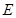 上的定点
上的定点
 作两条直线分别与轨迹
作两条直线分别与轨迹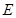 相交于
相交于 ,
,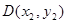 两点.试探究:当直线
两点.试探究:当直线 ,
, 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线 的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
 ,点
,点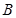 在直线
在直线 :
: 上运动,过点
上运动,过点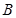 与
与 垂直的直线和线段
垂直的直线和线段 的垂直平分线相交于点
的垂直平分线相交于点 .
.(1)求动点
 的轨迹
的轨迹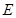 的方程;
的方程;(2)过(1)中的轨迹
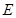 上的定点
上的定点
 作两条直线分别与轨迹
作两条直线分别与轨迹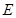 相交于
相交于 ,
,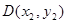 两点.试探究:当直线
两点.试探究:当直线 ,
, 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线 的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
的斜率是否为定值?若是,求出这个定值;若不是,说明理由.(1)  (2) 当直线
(2) 当直线 ,
, 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线 的斜率为定值
的斜率为定值
 (2) 当直线
(2) 当直线 ,
, 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线 的斜率为定值
的斜率为定值
试题分析:(1)由线段垂直平分线的性质知,
 ,所以动点
,所以动点 的轨迹
的轨迹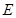 是以
是以 为焦点,直线
为焦点,直线 为准线的抛物线.易知其标准方程为
为准线的抛物线.易知其标准方程为 .
.设
 、
、 ,
,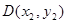 ,可由点差法求出
,可由点差法求出 ,
, ,
,
由直线
 ,
, 的倾斜角互补,得
的倾斜角互补,得


 定值
定值 试题解析:(1)依题意,得
 1分
1分∴动点
 的轨迹
的轨迹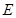 是以
是以 为焦点,直线
为焦点,直线 为准线的抛物线 3分
为准线的抛物线 3分∴动点
 的轨迹
的轨迹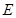 的方程为
的方程为 4分
4分(2)∵
 、
、 ,
,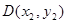 在抛物线
在抛物线 上
上∴
 5分
5分由①-②得,

∴直线
 的斜率为
的斜率为 7分
7分同理可得,直线
 的斜率为
的斜率为 9分
9分∴当直线
 ,
, 的倾斜角互补时,有
的倾斜角互补时,有
即

∴
 11分
11分由②-③得,

∴直线
 的斜率为
的斜率为 ④ 13分
④ 13分将
 代入④,得
代入④,得 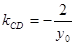
∴当直线
 ,
, 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线 的斜率为定值
的斜率为定值 14分
14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
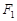 、
、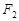 为双曲线
为双曲线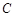 :
: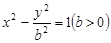 的左、右焦点,过
的左、右焦点,过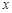 轴的直线,在
轴的直线,在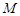 ,且
,且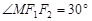 .圆
.圆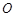 的方程是
的方程是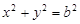 .
.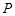 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为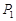 、
、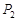 ,求
,求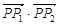 的值;
的值;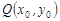 作圆
作圆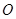 的切线
的切线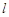 交双曲线
交双曲线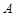 、
、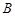 两点,
两点,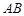 中点为
中点为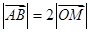 .
. 分别是椭圆
分别是椭圆 的左、右焦点, 点
的左、右焦点, 点 在椭圆上
在椭圆上 上.
上. 若
若 、
、 均与椭圆
均与椭圆 轴上是否存在定点
轴上是否存在定点 ,点
,点 的距离之积恒为1?若存在,请求出点
的距离之积恒为1?若存在,请求出点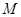 :
: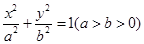 经过点
经过点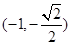 ,
,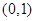 .
.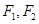 ,过点
,过点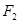 的直线交椭圆
的直线交椭圆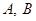 两点,求
两点,求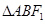 面积的最大值.
面积的最大值.
 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
 上的点到其两焦点距离之和为
上的点到其两焦点距离之和为 ,且过点
,且过点 .
.  为坐标原点,斜率为
为坐标原点,斜率为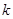 的直线过椭圆的右焦点,且与椭圆交于点
的直线过椭圆的右焦点,且与椭圆交于点 ,
,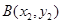 ,若
,若 ,求△
,求△ 的面积.
的面积. 的两个焦点为F1,F2,椭圆上一点M
的两个焦点为F1,F2,椭圆上一点M
 .
. 与椭圆恒有不同交点A,B,且
与椭圆恒有不同交点A,B,且 (O为坐标原点),求实数k的范围.
(O为坐标原点),求实数k的范围.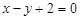 与曲线
与曲线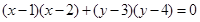 的交点个数是 .
的交点个数是 . 且和抛物线
且和抛物线 相切的直线
相切的直线 方程为 .
方程为 .