题目内容
在正三棱锥S-ABC中,D,E,F分别是SA,SC,AC的中点,P为SB上任意一点,则异面直线DE与PF所成的角的大小是( )
分析:根据正三棱锥的结构特征,证出DE⊥面SFB.由此对于任意FP,都有DE⊥FP,结果均为90°.
解答:解:如图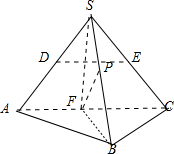
在正三棱锥S-ABC中,D,E,F分别是SA,SC,AC的中点,∴SF⊥AC,BF⊥AC,∴AC⊥面SFB.又DE∥AC,∴DE⊥面SFB.
又FP?面SFB.,∴DE⊥FP,∴异面直线DE与PF所成的角的大小是90°
故选D.

在正三棱锥S-ABC中,D,E,F分别是SA,SC,AC的中点,∴SF⊥AC,BF⊥AC,∴AC⊥面SFB.又DE∥AC,∴DE⊥面SFB.
又FP?面SFB.,∴DE⊥FP,∴异面直线DE与PF所成的角的大小是90°
故选D.
点评:本题是在正三棱锥S-ABC背景下考查异面直线夹角.解题过程中,应充分把握正三棱锥的结构特征,为问题解决提供丰富的几何平台.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
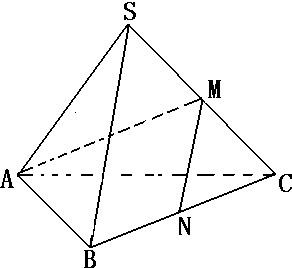 如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=| 3 |
| A、9π | B、12π |
| C、16π | D、32π |
在正三棱锥S-ABC中,D是AB的中点,且SD与BC成45°角,则SD与底面ABC所成角的正弦为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|