题目内容
在正三棱锥S-ABC中，若SA=4，BC=3，分别取SA、BC的中点E、F，则EF=分析：求线段EF的长可转化成求向量
的模，将
转化成
(
+
)进行求解，先求向量模的平方，然后再开方即可．
| EF |
| EF |
| 1 |
| 2 |
| AB |
| SC |
解答：解：因为|
|2=
=(
+
+
)=[
(
+
+2
)]2
=[
(
+
)]2=
(
+
)2=
(
+2
•
+
)
=
×(16+0+9)=
，所以|
|=
．
故答案为：
| EF |
| EF2 |
| 1 |
| 2 |
| SA |
| AB |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| SA |
| BC |
| AB |
=[
| 1 |
| 2 |
| AB |
| SC |
| 1 |
| 4 |
| AB |
| SC |
| 1 |
| 4 |
| AB2 |
| AB |
| SC |
| SC2 |
=
| 1 |
| 4 |
| 25 |
| 4 |
| EF |
| 5 |
| 2 |
故答案为：
| 5 |
| 2 |
点评：本题主要考查了空间两点之间的距离，以及利用向量求距离的方法，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
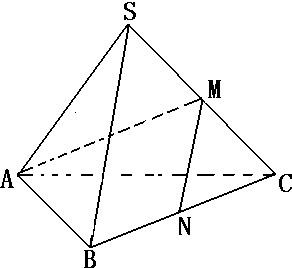如图，在正三棱锥S-ABC中，M、N分别为棱SC、BC的中点，并且AM⊥MN，若侧棱长SA=| 3 |
| A、9π | B、12π |
| C、16π | D、32π |
在正三棱锥S-ABC中，D是AB的中点，且SD与BC成45°角，则SD与底面ABC所成角的正弦为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|