题目内容
已知| e |
| a |
| e |
| a |
| e |
| a |
| e |
分析:先将“|
+
|=|
-2
|”转化为:“(
+
)2=(
-2
)2”,求得两向量的数量积,最后根据投影的定义,应用公式|
|cos<
,
>=
求解.
| a |
| e |
| a |
| e |
| a |
| e |
| a |
| e |
| a |
| a |
| b |
| a•b |
| |b| |
解答:解:∵|
+
|=|
-2
|,
∴(
+
)2=(
-2
)2
∴
2 +2
+
2=
2 -4
+(4
)2
∴
=
又∵|
|=1
∴向量
在
方向上的投影为:
=
故答案为:
| a |
| e |
| a |
| e |
∴(
| a |
| e |
| a |
| e |
∴
| a |
| e |
| a |
| e |
| a |
| e |
| a |
| e |
∴
| a |
| e |
| 1 |
| 2 |
又∵|
| e |
∴向量
| a |
| e |
| ||||
|
|
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查向量投影的定义及求解的方法,公式与定义两者要灵活运用.

练习册系列答案
相关题目
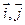 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设 ,
, 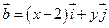 且满足
且满足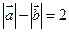
 (x,y)的轨迹E的方程.
(x,y)的轨迹E的方程.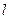 过点
过点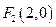 且法向量为
且法向量为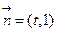 ,直线与轨迹E交于
,直线与轨迹E交于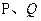 两点.点
两点.点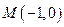 ,无论直线
,无论直线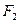 怎样转动,
怎样转动, 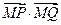 是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数
是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数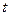 的取值范围;
的取值范围;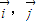 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设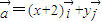 ,
,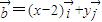 ,且满足
,且满足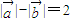
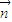 =(t,1),直线与轨迹E交于P、Q两点.点M(-1,0),无论直线l绕点F2怎样转动,
=(t,1),直线与轨迹E交于P、Q两点.点M(-1,0),无论直线l绕点F2怎样转动,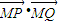 是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数t的取值范围.
是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数t的取值范围. 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设
 =
= ,
,

 =,且满足
=,且满足
 过点
过点
 且法向量为
且法向量为 ,直线与轨迹
,直线与轨迹 交于
交于 两点.点
两点.点 ,无论直线
,无论直线 是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数
是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数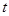 的取值范围;(9分)
的取值范围;(9分)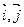 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设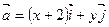
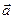 =
=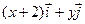 ,
, 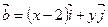
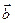 =,且满足
=,且满足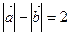
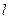 过点
过点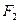
 且法向量为
且法向量为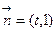 ,直线与轨迹
,直线与轨迹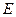 交于
交于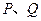 两点.点
两点.点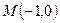 ,无论直线
,无论直线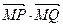 是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数
是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数 的取值范围;(9分)
的取值范围;(9分)