题目内容
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.

(1)求证AC⊥平面DEF;
(2)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N的位置;若不存在,试说明理由.
(3)求平面ABD与平面DEF所成锐二面角的余弦值。
【答案】
解(证明)(1)∵AB⊥平面BCD,∴AB⊥BC,AB⊥BD.
∵△BCD是正三角形,且AB=BC=a,∴AD=AC= .
.
设G为CD的中点,则CG= ,AG=
,AG=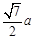 .
.
∴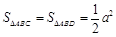 ,
, ,
, .
.
三棱锥D-ABC的表面积为 .
.
(2)取AC的中点H,∵AB=BC,∴BH⊥AC.
∵AF=3FC,∴F为CH的中点.
∵E为BC的中点,∴EF∥BH.则EF⊥AC.
∵△BCD是正三角形,∴DE⊥BC.
∵AB⊥平面BCD,∴AB⊥DE.
∵AB∩BC=B,∴DE⊥平面ABC.∴DE⊥AC.
∵DE∩EF=E,∴AC⊥平面DEF.
(3)存在这样的点N,
当CN= 时,MN∥平面DEF.
时,MN∥平面DEF.
连CM,设CM∩DE=O,连OF.
由条件知,O为△BCD的重心,CO= CM.
CM.
∴当CF= CN时,MN∥OF.∴CN=
CN时,MN∥OF.∴CN=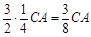 .
.
【解析】略

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
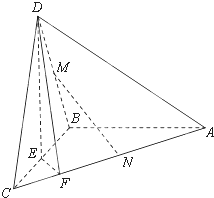 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.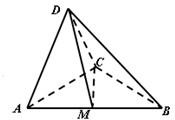 如图,在三棱锥D-ABC中,△ADC,△ACB均为等腰直角三角形AD=CD=
如图,在三棱锥D-ABC中,△ADC,△ACB均为等腰直角三角形AD=CD=

