题目内容
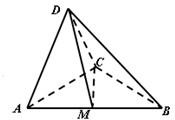 如图,在三棱锥D-ABC中,△ADC,△ACB均为等腰直角三角形AD=CD=
如图,在三棱锥D-ABC中,△ADC,△ACB均为等腰直角三角形AD=CD=| 2 |
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求异面直线BD与CM所成角的余弦值;
(Ⅲ)求二面角A-CD-M的余弦值.
分析:(Ⅰ)要证明BC⊥平面ACD.我们根据可以根据已知中侧面ADC⊥底面ABC.结合平面与平面垂直的性质定理进行证明,即只要说明AC⊥BC即可,由(1)的结论,取AC的中点为O,连接DO,OM.建立空间直角坐标系O-xyz,然后利用空间向量法,进行求解.
(Ⅱ)要求异面直线BD与CM所成角的余弦值,我们只要求
与
夹角余弦值的绝对值即可.
(Ⅲ)要求锐二面角A-CD-M的余弦值,我们只要求出平面ACD的法向量与平面MCD的法向量夹角余弦值的绝对值即可.
(Ⅱ)要求异面直线BD与CM所成角的余弦值,我们只要求
| BD |
| CM |
(Ⅲ)要求锐二面角A-CD-M的余弦值,我们只要求出平面ACD的法向量与平面MCD的法向量夹角余弦值的绝对值即可.
解答: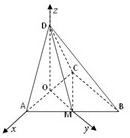 解:(Ⅰ)证明:因为AC⊥BC,平面ADC⊥平面ABC,
解:(Ⅰ)证明:因为AC⊥BC,平面ADC⊥平面ABC,
平面ADC∩平面ABC=AC,BC?平面ABC,
所以BC⊥平面ACD.
(Ⅱ)取AC的中点为O,连接DO,OM.
建立空间直角坐标系O-xyz如图所示.
则A(1,0,0),C(-1,0,0),D(0,0,1),
B(-1,2,0),M(0,1,0).
=(1,-2,1),
=(1,1,0),
cos<
,
>=
=
=-
所以异面直线BD与CM所成角的余弦值为
.
(Ⅲ)平面ACD的法向量为
1=(0,1,0),
设平面MCD的法向量为
2=(x,y,z),
=(1,0,1),
=(1,1,0)
由
,得
,取x=-1,得y=z=1,
所以
2=(-1,1,1).
cos<
1,
2>=
=
=
所以,二面角A-CD-M的余弦值为
.
 解:(Ⅰ)证明:因为AC⊥BC,平面ADC⊥平面ABC,
解:(Ⅰ)证明:因为AC⊥BC,平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,BC?平面ABC,
所以BC⊥平面ACD.
(Ⅱ)取AC的中点为O,连接DO,OM.
建立空间直角坐标系O-xyz如图所示.
则A(1,0,0),C(-1,0,0),D(0,0,1),
B(-1,2,0),M(0,1,0).
| BD |
| CM |
cos<
| BD |
| CM |
| ||||
|
|
| 1-2+0 | ||||
|
| ||
| 6 |
所以异面直线BD与CM所成角的余弦值为
| ||
| 6 |
(Ⅲ)平面ACD的法向量为
| n |
设平面MCD的法向量为
| n |
| CD |
| CM |
由
|
|
所以
| n |
cos<
| n |
| n |
| ||||
|
|
| 1 | ||
|
| ||
| 3 |
所以,二面角A-CD-M的余弦值为
| ||
| 3 |
点评:空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
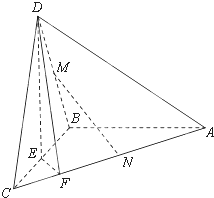 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.

