题目内容
已知直线l:mx-y+1-m=0与圆C:x2+(y-1)2=5交于A、B两点;
(Ⅰ)若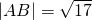 ,求直线l的倾斜角;
,求直线l的倾斜角;
(Ⅱ)求弦AB的中点M的轨迹方程;
(Ⅲ)圆C上是否存在一点P使得△ABP为等边三角形?若存在,求出P点坐标;不存在,请说明理由.
解:(Ⅰ)圆心C(0,1)到直线的距离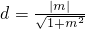 ,
,
所以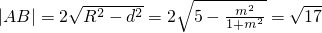 ,解得
,解得 ,
,
所以,倾角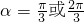 ;…(4分)
;…(4分)
(Ⅱ)直线l过定点N(1,1),设动点M(x,y),则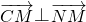 ,
,
所以(x,y-1)•(x-1,y-1)=0,化简得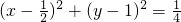 ;…(9分)
;…(9分)
(Ⅲ)不存在.假设存在符合条件的P点,则由△ABP是等边三角形知,
其外接圆与内切圆的圆心均C(0,1),外接圆半径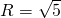 ,
,
内切圆半径r等于圆心(0,1)到直线AB的距离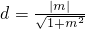 ,
,
又由等边三角形的性质得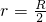 ,所以有
,所以有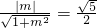 ,
,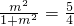 ,m无解,故不存在这样的点P.…(13分)
,m无解,故不存在这样的点P.…(13分)
分析:(Ⅰ)直接利用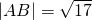 ,圆心到直线的距离,半径满足勾股定理,求出m的值,即可求直线l的倾斜角;
,圆心到直线的距离,半径满足勾股定理,求出m的值,即可求直线l的倾斜角;
(Ⅱ)设出动点坐标,利用垂直关系,数量积为0,直接求弦AB的中点M的轨迹方程;
(Ⅲ)通过由△ABP是等边三角形,其外接圆与内切圆的圆心相同,通过外接圆半径,内切圆半径r等于圆心到直线AB的距离,推出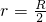 ,方程无解,则不存在否则存在.
,方程无解,则不存在否则存在.
点评:本题考查轨迹方程分求法,点到直线的距离公式的应用,直线的倾斜角的求法,考查计算能力,转化思想.
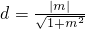 ,
,所以
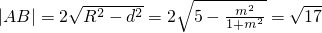 ,解得
,解得 ,
,所以,倾角
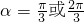 ;…(4分)
;…(4分)(Ⅱ)直线l过定点N(1,1),设动点M(x,y),则
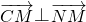 ,
,所以(x,y-1)•(x-1,y-1)=0,化简得
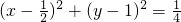 ;…(9分)
;…(9分)(Ⅲ)不存在.假设存在符合条件的P点,则由△ABP是等边三角形知,
其外接圆与内切圆的圆心均C(0,1),外接圆半径
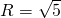 ,
,内切圆半径r等于圆心(0,1)到直线AB的距离
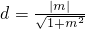 ,
,又由等边三角形的性质得
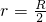 ,所以有
,所以有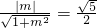 ,
,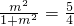 ,m无解,故不存在这样的点P.…(13分)
,m无解,故不存在这样的点P.…(13分)分析:(Ⅰ)直接利用
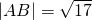 ,圆心到直线的距离,半径满足勾股定理,求出m的值,即可求直线l的倾斜角;
,圆心到直线的距离,半径满足勾股定理,求出m的值,即可求直线l的倾斜角;(Ⅱ)设出动点坐标,利用垂直关系,数量积为0,直接求弦AB的中点M的轨迹方程;
(Ⅲ)通过由△ABP是等边三角形,其外接圆与内切圆的圆心相同,通过外接圆半径,内切圆半径r等于圆心到直线AB的距离,推出
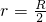 ,方程无解,则不存在否则存在.
,方程无解,则不存在否则存在.点评:本题考查轨迹方程分求法,点到直线的距离公式的应用,直线的倾斜角的求法,考查计算能力,转化思想.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,在平面直角坐标系xoy中,已知“葫芦”曲线C由圆弧C1与圆弧C2相接而成,两相接点M,N均在直线y=-
如图,在平面直角坐标系xoy中,已知“葫芦”曲线C由圆弧C1与圆弧C2相接而成,两相接点M,N均在直线y=- 上.圆弧C1所在圆的圆心是坐标原点O,半径为r1=2;圆弧C2过点A(0,-6
上.圆弧C1所在圆的圆心是坐标原点O,半径为r1=2;圆弧C2过点A(0,-6 ).
). =0与“葫芦”曲线C交于E,F两点.当|EF|=4+4
=0与“葫芦”曲线C交于E,F两点.当|EF|=4+4 时,求直线l的方程.
时,求直线l的方程.