题目内容
（2012•洛阳一模）在直角坐标系中，如果不同的两点A（a，b），B（-a，-b）在函数y=f（x）的图象上，那么称[A，B]为该函数的一组关于原点的中心对称点（[A，B]与[B，A]看作一组），函数f（x）=
关于原点的中心对称点的组数为（ ）
|
分析：作出y=sinx，x≤0关于原点的对称图形C，则y=|lgx|的图象与C交点个数即为所求的组数．
解答：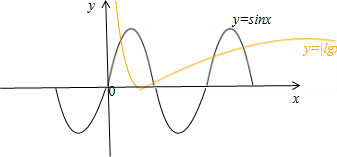
解：由于y=sinx，x∈R的图象关于原点对称，由已知，y=|lgx|的图象与y=sinx，x∈R在y轴左侧图象交点个数
即为所求的组数．在同一坐标系内两图象如图所示，
共有四个交点，所以关于原点的中心对称点的组数为4
故选C
解：由于y=sinx，x∈R的图象关于原点对称，由已知，y=|lgx|的图象与y=sinx，x∈R在y轴左侧图象交点个数即为所求的组数．在同一坐标系内两图象如图所示，
共有四个交点，所以关于原点的中心对称点的组数为4
故选C
点评：本题给出分段函数，求函数关于原点的中心对称点的组数．着重考查了三角函数、对数函数的图象与性质等知识，属于中档题．
练习册系列答案
相关题目