题目内容
已知二次函数f(x)=ax2+bx+c的图像的顶点坐标是(![]() ,-
,-![]() ),且f(3)=2
),且f(3)=2
(Ⅰ)求y=f(x)的表达式,并求出f(1),f(2)的值;
(Ⅱ)数列{an},{bn},若对任意的实数x都满足g(x)·f(x)+anx+bn=xn+1,n∈N*,其中g(x)是定义在实数R上的一个函数,求数列{an}、{bn}的通项公式;
(Ⅲ)设圆Cn:(x-an)2+(y-bn)2=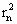 ,若圆Cn与圆Cn+1外切,{rn}是各项都是正数的等比数列,记Sn是前n个圆的面积之和,求
,若圆Cn与圆Cn+1外切,{rn}是各项都是正数的等比数列,记Sn是前n个圆的面积之和,求![]()
![]() .(n∈N*)
.(n∈N*)
答案:
解析:
解析:
|
解:(Ⅰ)由已知得f(x)=a(x- ∴a=1 ∴f(x)=x2-3x+2,x∈R f(1)=0,f(2)=0 (Ⅱ)g(1)·f(1)+an+bn=1n+1 即an+bn=1 ① g(2)·f(2)+2an+bn=2n+1 即2an+bn=2n+1 ② 由①②得an=2n+1-1,bn=2-2n+1, (Ⅲ)|Cn+1Cn|= ∴rn+1(1+q)= Sn=π( ∴ |

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
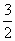 )2-
)2-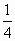 ,a≠0,∴f(3)=a(3-
,a≠0,∴f(3)=a(3-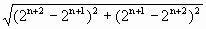 =
=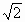 ·2n+1,设数列{rn}的公比为q,则rn+rn+1=rn(1+q)=|Cn+1Cn|=
·2n+1,设数列{rn}的公比为q,则rn+rn+1=rn(1+q)=|Cn+1Cn|=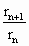 =2 ∴rn=
=2 ∴rn=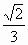 ·2n+1 ∴
·2n+1 ∴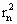 =
=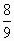 ·4n
·4n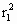 +
+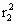 +
+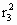 +…+
+…+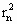 )=
)=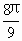 ·(41+42+…+4n)=
·(41+42+…+4n)=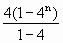 =
=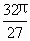 (4n-1)
(4n-1)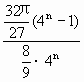 =
=