题目内容
已知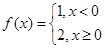 ,
,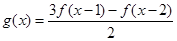 .
.
(1)当 ;
;
(2)当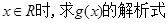 ,并画出其图象;
,并画出其图象;
(3)求方程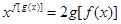 的解.
的解.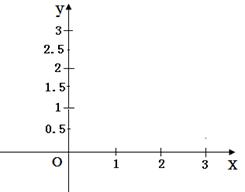
解:(1) g(x)=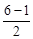 =
=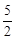 .
.
(2)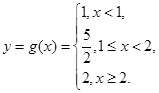 其图象如右图.
其图象如右图. 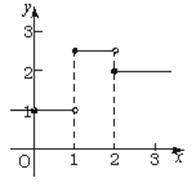
(3)x=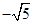 或x=2.
或x=2.
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知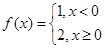 ,
,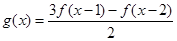 .
.
(1)当 ;
;
(2)当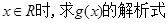 ,并画出其图象;
,并画出其图象;
(3)求方程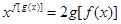 的解.
的解.
解:(1) g(x)=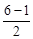 =
=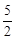 .
.
(2)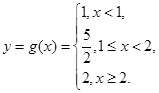 其图象如右图.
其图象如右图. 
(3)x=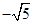 或x=2.
或x=2.
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案