题目内容
在公差不为零的等差数列{an}与等比数列{bn}中,设a1=1,a1=b1,a2=b2,a8=b3.(1)求公差和公比.
(2)是否存在常数a、b∈R,使对一切n∈N,都有an=logabn+b成立?若存在,求之;若不存在,请说明理由.
解:(1)设{an}的公差为d,{bn}的公比为q,则有
a2=b2![]() 1+d=q, ①
1+d=q, ①
a8=b3![]() 1+7d=q2. ②
1+7d=q2. ②
由①②解得q=6,d=5.
(2)∵a1=1,b1=a1=1,d=5,q=6,
∴an=5n-4,bn=6n-1.
假设存在a、b,使n∈N,都有an=logabn+b,
∴5n-4=loga6n-1+b.
∴(5-loga6)n+(loga6-b-4)=0,得
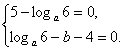
解得a=![]() ,b=1.
,b=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在公差不为零的等差数列{an}中,若S8是S4的3倍,则a1与d的比为:( )
| A、5:2 | B、2:5 | C、5:1 | D、1:5 |
在公差不为零的等差数列{an}中,S10=4S5,则a1:d等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |