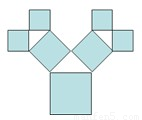
题目内容
如图所示是毕达哥拉斯的生长程序：正方形一边上连结着等腰直角三角形，等腰直角三角形两直角边再分别连结着一个正方形，如此继续下去，共得到127个正方形.若最后得到的正方形的边长为1，则初始正方形的边长为_____________.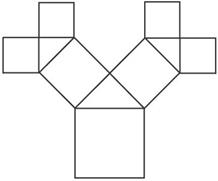
8 设共形成n种正方形,则1+2+22+…+2n-1=127,
∴
=127.∴n=7.设n种正方形的边长构成数列{an},且{an}为等比数列,a7=1,q=
.
∴a7=a1·q6.∴a1=
=
=8.
练习册系列答案
相关题目
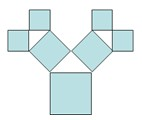如图所示是毕达哥拉斯的生长程序：正方形上连接着一个等腰直角三角形，等腰直角三角形的直角边上再连接正方形…，如此继续．若共得到1023个正方形，设起始正方形的边长为
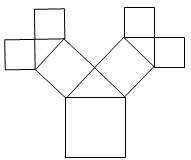如图所示是毕达哥拉斯的生长程序：正方形一边上连接着等腰直角三角形，等腰直角三角形两直角边再分别连接着一个正方形，如此继续下去，共得到127个正方形．若最后得到的正方形的边长为1，则初始正方形的边长为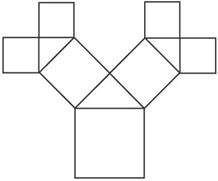
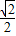，则最小正方形的边长为 ．