题目内容
在平面直角坐标系xoy中,已知直线l:8x+6y+1=0,圆C1:x2+y2+8x-2y+13=0,圆C2:x2+y2+8tx-8y+16t+12=0.
(1)当t=-1时,试判断圆C1与圆C2的位置关系,并说明理由;
(2)若圆C1与圆C2关于直线l对称,求t的值;
(3)在(2)的条件下,若P(a,b)为平面上的点,是否存在过点P的无穷多对互相垂直的直线l1和l2,它们分别与圆C1与圆C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,若存在,求点P的坐标,若不存在,请说明理由.
解:(1)t=-1时,圆C1的圆心C1(-4,1),半径r1=2;圆C2的圆心C2(4,4),半径r2=2
∴圆心距|C1C2|= >r1+r2=8
>r1+r2=8
∴两圆相离
(2)圆C2的圆心C2(-4t,4),半径r2=
∵圆C1与圆C2关于直线l对称,又直线l的斜率
由 得t=0;,
得t=0;,
(3)假设存在P(a,b)满足条件:不妨设l1的方程为y-b=k(x-a)(k≠0)
则l2的方程为y-b=-
因为圆C1与圆C2的半径相等,又直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,
所以圆C1的圆心到直线l1距离,和圆C2的圆心到直线l2的距离相等,
即 =
=
整理得|(a+4)k-b+1|=|(b-4)k+a|
即(a+4)k-b+1=(b-4)k+a或(a+4)k-b+1=(4-b)k-a
即(a-b+8)k-a-b+1=0或(a+b)k+a-b+1=0
因为k取值无穷多个
所以 或
或
解得 或
或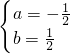
∴这样的点P可能是P1(- ),P2(-
),P2(- )
)
∴所求点P的坐标为(- )和(-
)和(- ).
).
分析:(1)求得两圆的圆心距,与半径半径,即可求得结论;
(2)确定圆C2的圆心与半径,两圆圆C1与圆C2关于直线l对称,直线l的斜率,可求t的值;
(3)利用圆C1与圆C2的半径相等,又直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,可得圆C1的圆心到直线l1距离,和圆C2的圆心到直线l2的距离相等,由此可得结论.
点评:本题考查圆与圆的位置关系,考查圆的对称性,考查存在性问题的探求,考查学生分析解决问题的能力,属于中档题.
∴圆心距|C1C2|=
 >r1+r2=8
>r1+r2=8∴两圆相离
(2)圆C2的圆心C2(-4t,4),半径r2=

∵圆C1与圆C2关于直线l对称,又直线l的斜率

由
 得t=0;,
得t=0;,(3)假设存在P(a,b)满足条件:不妨设l1的方程为y-b=k(x-a)(k≠0)
则l2的方程为y-b=-

因为圆C1与圆C2的半径相等,又直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,
所以圆C1的圆心到直线l1距离,和圆C2的圆心到直线l2的距离相等,
即
 =
=
整理得|(a+4)k-b+1|=|(b-4)k+a|
即(a+4)k-b+1=(b-4)k+a或(a+4)k-b+1=(4-b)k-a
即(a-b+8)k-a-b+1=0或(a+b)k+a-b+1=0
因为k取值无穷多个
所以
 或
或
解得
 或
或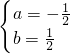
∴这样的点P可能是P1(-
 ),P2(-
),P2(- )
)∴所求点P的坐标为(-
 )和(-
)和(- ).
).分析:(1)求得两圆的圆心距,与半径半径,即可求得结论;
(2)确定圆C2的圆心与半径,两圆圆C1与圆C2关于直线l对称,直线l的斜率,可求t的值;
(3)利用圆C1与圆C2的半径相等,又直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,可得圆C1的圆心到直线l1距离,和圆C2的圆心到直线l2的距离相等,由此可得结论.
点评:本题考查圆与圆的位置关系,考查圆的对称性,考查存在性问题的探求,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.