题目内容
集合A={(x,y)|y=a},B={(x,y)|y=bx+1,b>0,b≠1},若A∩B只有一个子集,则实数a的取值范围是 .
【答案】分析:集合A是一条直线,集合B是一条曲线,作出图象,利用集合A∩B只有一个子集,能求出实数a的取值范围.
解答:解:集合A={(x,y)|y=a}是一条直线,
集合B={(x,y)|y=bx+1,b>0,b≠1}是一条曲线,
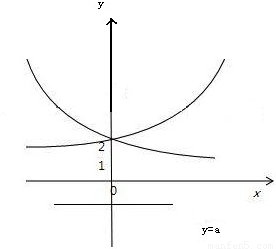
∵集合A∩B只有一个子集,∴A∩B=∅,如图.
所以a的范围是:a≤1
故答案为:(-∞,1].
点评:本题考查交集及其运算,是基础题.解题时要认真审题,仔细解答,注意数形结合思想的合理运用.
解答:解:集合A={(x,y)|y=a}是一条直线,
集合B={(x,y)|y=bx+1,b>0,b≠1}是一条曲线,
∵集合A∩B只有一个子集,∴A∩B=∅,如图.
所以a的范围是:a≤1
故答案为:(-∞,1].

点评:本题考查交集及其运算,是基础题.解题时要认真审题,仔细解答,注意数形结合思想的合理运用.

练习册系列答案
相关题目
设集合A=B={(x,y)|x∈R,y∈R},从A到B的映射f:(x,y)→(x+2y,2x-y),则在映射f下B中的元素(1,1)对应的A中元素为( )
| A、(1,3) | ||||
| B、(1,1) | ||||
C、(
| ||||
D、(
|