题目内容
若z是实系数方程x2-2x+p=0的一个虚根,且|z|=2,则p=
- A.2
- B.3
- C.4
- D.5
C
分析:设出复数z,利用已知条件,结合韦达定理,及|z|=2,求得p.
解答:设z=a+bi,则方程的另一个根为z'=a-bi,且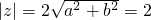
由韦达定理直线z+z'=2a=-2,∴a=-1,∴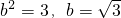
∴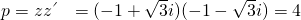 .
.
故选C.
点评:本题的考点是一元二次方程的根与系数的关系,主要考查复数代数形式乘除运算,韦达定理的使用,复数的模,是中档题.
分析:设出复数z,利用已知条件,结合韦达定理,及|z|=2,求得p.
解答:设z=a+bi,则方程的另一个根为z'=a-bi,且
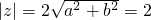
由韦达定理直线z+z'=2a=-2,∴a=-1,∴
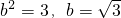
∴
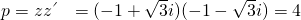 .
.故选C.
点评:本题的考点是一元二次方程的根与系数的关系,主要考查复数代数形式乘除运算,韦达定理的使用,复数的模,是中档题.

练习册系列答案
相关题目