题目内容
从椭圆短轴的一个端点看长轴两个端点的视角为120°,那么此椭圆的离心率为 .
【答案】分析:利用椭圆的长轴为A1A2,B为短轴一端点,若∠A1BA2=120°,求出a,b的关系,利用a2-c2=b2求出a,c的关系,求出椭圆的离心率即可.
解答: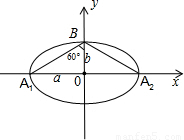 解:因为椭圆的长轴为A1A2,B为短轴一端点,∵∠A1BA2=120°,
解:因为椭圆的长轴为A1A2,B为短轴一端点,∵∠A1BA2=120°,
所以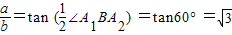 ,
,
即a2=3b2,又a2-c2=b2,
∴2a2=3c2,
解得e=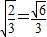 ;
;
故答案为: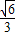 .
.
点评:本题考查椭圆的基本性质,注意椭圆中元素的几何意义,考查计算能力.
解答:
 解:因为椭圆的长轴为A1A2,B为短轴一端点,∵∠A1BA2=120°,
解:因为椭圆的长轴为A1A2,B为短轴一端点,∵∠A1BA2=120°,所以
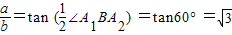 ,
,即a2=3b2,又a2-c2=b2,
∴2a2=3c2,
解得e=
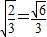 ;
;故答案为:
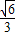 .
.点评:本题考查椭圆的基本性质,注意椭圆中元素的几何意义,考查计算能力.

练习册系列答案
相关题目