题目内容
从椭圆短轴的一个端点看长轴的两个端点的视角为120°,那么此椭圆的离心率为( )
分析:结合图形,得出a、b之间的关系,再根据a2=b2+c2推导出a、c之间的关系,根据e=
求解即可.
| c |
| a |
解答: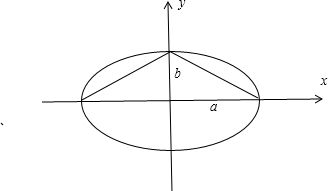 解:∵从椭圆的短轴的一个端点看长轴的两个端点的视角为120°,
解:∵从椭圆的短轴的一个端点看长轴的两个端点的视角为120°,
∴tan60°=
=
,
∴a2=3b2=3(a2-c2),即2a2=3c2,
得到
=
,
∴e=
=
.
故选D
 解:∵从椭圆的短轴的一个端点看长轴的两个端点的视角为120°,
解:∵从椭圆的短轴的一个端点看长轴的两个端点的视角为120°,∴tan60°=
| a |
| b |
| 3 |
∴a2=3b2=3(a2-c2),即2a2=3c2,
得到
| c2 |
| a2 |
| 2 |
| 3 |
∴e=
| c |
| a |
| ||
| 3 |
故选D
点评:本题考查椭圆的离心率,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目