题目内容
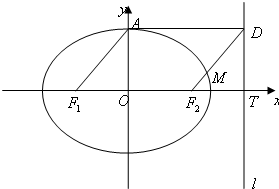
如图,已知椭圆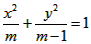 (2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线交于A、B、C、D,设f (m)=||AB|-|CD| |。
(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线交于A、B、C、D,设f (m)=||AB|-|CD| |。
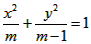 (2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线交于A、B、C、D,设f (m)=||AB|-|CD| |。
(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线交于A、B、C、D,设f (m)=||AB|-|CD| |。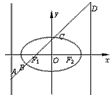
(1)求f (m)的解析式;
(2)求f (m)的最大、最小值。
解:(1)设椭圆的焦距为c,则c2=m-(m-1)=1,则 F1(-1,0),F2(1,0),
椭圆的准线为x=±m,直线的方程为y=x+1 易知A(-m,-m+1),B(m,m-1)
由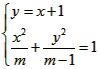 ,消去y并整理得:(2m-1)x2+2mx+2m-m2=0,
,消去y并整理得:(2m-1)x2+2mx+2m-m2=0,
△=8m(m-1)2,∵ m∈[2,5],∴△>0恒成立
此时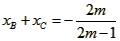 ,又直线的斜率k=1,
,又直线的斜率k=1,
∴|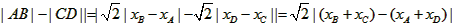 ,
,
又xA=-m,xD=m,∴xA+xD=0,
故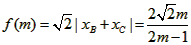 m∈[2,5];
m∈[2,5];
(2) ,又m∈[2,5],易知
,又m∈[2,5],易知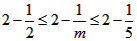 ,
,
∴ ,故
,故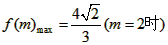 ,
,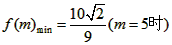
椭圆的准线为x=±m,直线的方程为y=x+1 易知A(-m,-m+1),B(m,m-1)
由
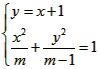 ,消去y并整理得:(2m-1)x2+2mx+2m-m2=0,
,消去y并整理得:(2m-1)x2+2mx+2m-m2=0,△=8m(m-1)2,∵ m∈[2,5],∴△>0恒成立
此时
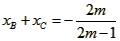 ,又直线的斜率k=1,
,又直线的斜率k=1,∴|
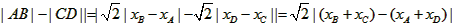 ,
,又xA=-m,xD=m,∴xA+xD=0,
故
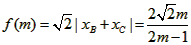 m∈[2,5];
m∈[2,5];(2)
 ,又m∈[2,5],易知
,又m∈[2,5],易知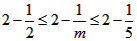 ,
, ∴
 ,故
,故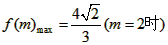 ,
,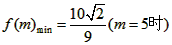

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,已知椭圆
如图,已知椭圆 如图,已知椭圆C:
如图,已知椭圆C: 如图,已知椭圆的中心在原点,焦点在x轴上,离心率为
如图,已知椭圆的中心在原点,焦点在x轴上,离心率为 如图,已知椭圆C:
如图,已知椭圆C: