题目内容
在直角坐标系xOy中,直线l的方程为x-y+4=0,曲线C的参数方程为 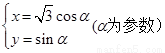 .
.
(Ⅰ)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,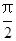 ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(Ⅱ)设点Q是曲线C上的一个动点,求它到直线l的距离的最值;
(Ⅲ)请问是否存在直线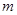 ,
,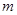 ∥l且
∥l且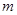 与曲线C的交点A、B满足
与曲线C的交点A、B满足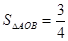 ;
;
若存在请求出满足题意的所有直线方程,若不存在请说明理由。
【答案】
(I)点P在直线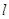 上.
上.
(II)当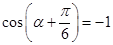 时,d取得最小值,且最小值为
时,d取得最小值,且最小值为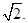
当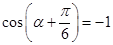 时,d取得最大值,且最大值为3
时,d取得最大值,且最大值为3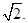
(Ⅲ)满足题意直线m有4条,方程为: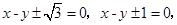 。
。
【解析】
试题分析:(I)把极坐标系下的点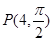 化为直角坐标,得P(0,4)2分
化为直角坐标,得P(0,4)2分
因为点P的直角坐标(0,4)满足直线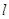 的方程
的方程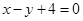 ,所以点P在直线
,所以点P在直线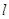 上.4分
上.4分
(II)因为点Q在曲线C上,故可设点Q的坐标为 ,5分
,5分
从而点Q到直线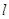 的距离为
的距离为
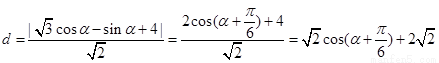 , 6分
, 6分
由此得,当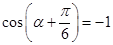 时,d取得最小值,且最小值为
时,d取得最小值,且最小值为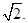
当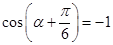 时,d取得最大值,且最大值为3
时,d取得最大值,且最大值为3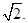 8分
8分
(Ⅲ)设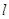 平行线m方程:x-y+n =
0 9分
平行线m方程:x-y+n =
0 9分
椭圆与直线方程联立再由弦长公式得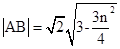
设O到直线m的距离为d,则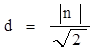 10分
10分
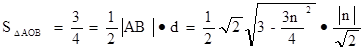
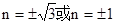 经验证均满足题意
经验证均满足题意
所以满足题意直线m有4条,方程为: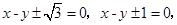 12分
12分
考点:点的极坐标,椭圆的参数方程,直线与椭圆的位置关系,直线方程。
点评:中档题,本题综合性较强,涉及直线与椭圆的位置关系,通过建立方程组,应用韦达定理、弦长公式等,进一步表示出三角形面积,从而建立“变量”的方程,达到解题目的。思路比较明确。

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为