题目内容
已知函数f(x)=2sinxcos(x+ )-cos2x+m.
)-cos2x+m.
(I)求函数f(x)的最小正周期;
(Ⅱ)当x∈[- ,
, ]时,函数f(x)的最小值为-3,求实数m的值.
]时,函数f(x)的最小值为-3,求实数m的值.
解:(I)∵f(x)=2sinx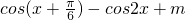 =
=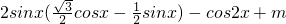 =
=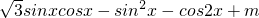 =
=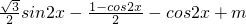 (3分)
(3分)
=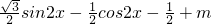 =sin(2x-
=sin(2x- )+m-
)+m- .(5分)
.(5分)
∴f(x)的最小正周期 (6分)
(6分)
(Ⅱ)当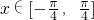 ,有
,有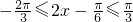 (8分)
(8分)
∴ .(10分)
.(10分)
得到f(x)的最小值为m .(11分)
.(11分)
由已知,有m =-3则m=
=-3则m= (12分)
(12分)
分析:(I)先利用和差角公式及辅助角公式对函数进行化简可得,f(x)=sin(2x- )+m-
)+m- ,根据周期公式可求,
,根据周期公式可求,
(II)由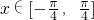 ,可得
,可得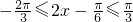 结合正弦函数的性质可求
结合正弦函数的性质可求 ,求出函数的f(x)的最小值为m
,求出函数的f(x)的最小值为m ,根据已知可求m.
,根据已知可求m.
点评:本题主要考查了三角函数的和差角公式及辅助角公式的应用,三角函数的性质的考查,关键是要熟练掌握基础知识,灵活应用.
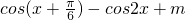 =
=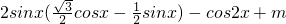 =
=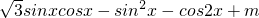 =
=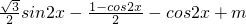 (3分)
(3分)=
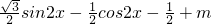 =sin(2x-
=sin(2x- )+m-
)+m- .(5分)
.(5分)∴f(x)的最小正周期
 (6分)
(6分)(Ⅱ)当
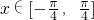 ,有
,有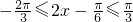 (8分)
(8分)∴
 .(10分)
.(10分)得到f(x)的最小值为m
 .(11分)
.(11分)由已知,有m
 =-3则m=
=-3则m= (12分)
(12分)分析:(I)先利用和差角公式及辅助角公式对函数进行化简可得,f(x)=sin(2x-
 )+m-
)+m- ,根据周期公式可求,
,根据周期公式可求,(II)由
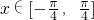 ,可得
,可得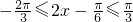 结合正弦函数的性质可求
结合正弦函数的性质可求 ,求出函数的f(x)的最小值为m
,求出函数的f(x)的最小值为m ,根据已知可求m.
,根据已知可求m.点评:本题主要考查了三角函数的和差角公式及辅助角公式的应用,三角函数的性质的考查,关键是要熟练掌握基础知识,灵活应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目