题目内容
如图所示，在边长为a的正方形组成的网格中，设椭圆C1、C2、C3的离心率分别为e1、e2、e3，则e1、e2、e3的关系为 ．
【答案】分析：根据图形分别得到椭圆C1、C2、C3的长轴长和短轴长，利用椭圆的离心率公式和平方关系分别算出e1、e2、e3的值或范围，再加以比较即可得到本题的答案．
解答：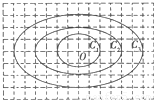
解：先看椭圆C1，长轴2a1=4a，短轴2b1∈（2a，4a）
∴离心率e1=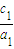
∈（0，
）
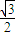椭圆C2，长轴2a1=8a，短轴2b2=4a
∴离心率e2=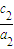
=
=
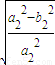同理可得椭圆C3的离心率e3=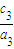
=
=
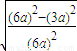∴e1、e2、e3的关系为e1＜e2=e3
故答案为：e1＜e2=e3
点评：本题给出正方形方格内的一些椭圆，比较它们离心率的大小．着重考查了椭圆基本量的平方关系和椭圆的离心率公式等知识，属于基础题．
解答：
解：先看椭圆C1，长轴2a1=4a，短轴2b1∈（2a，4a）∴离心率e1=
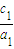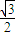∈（0，）椭圆C2，长轴2a1=8a，短轴2b2=4a
∴离心率e2=
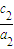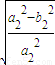==同理可得椭圆C3的离心率e3=
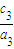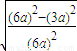==∴e1、e2、e3的关系为e1＜e2=e3
故答案为：e1＜e2=e3
点评：本题给出正方形方格内的一些椭圆，比较它们离心率的大小．着重考查了椭圆基本量的平方关系和椭圆的离心率公式等知识，属于基础题．
练习册系列答案
相关题目
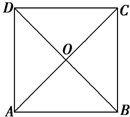如图所示，在边长为4的正方形纸片ABCD中，AC与BD相交于O，剪去△AOB，将剩余部分沿OC、OD折叠，使OA、OB重合，则以A、（B）、C、D、O为顶点的四面体的体积为
如图所示，在边长为a的正方形组成的网格中，设椭圆C1、C2、C3的离心率分别为e1、e2、e3，则e1、e2、e3的关系为
（2012•福建）如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为（ ）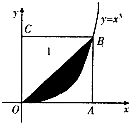
（2013•临沂一模）如图所示，在边长为l的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为（ ）