题目内容
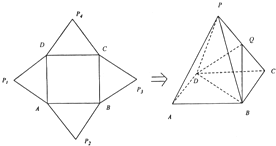 如图,正方形ABCD的边长为2,将四条边对应的第腰三角形折起构成一个正四棱锥P-ABCD.
如图,正方形ABCD的边长为2,将四条边对应的第腰三角形折起构成一个正四棱锥P-ABCD.(1)当Q为PC为中点时,证明PA∥平面BDQ;
(2)当等腰三角形的腰长为多少时,异面直线PA与BC所成的角为60°;
(3)当侧棱与底面所成的角为60°时,求相邻两个侧面所成的二面角的余弦值.
分析:(1)要证PA∥平面BDQ,根据Q为PC的中点,可想到连结AC交BD于O,连结OQ,然后利用三角形中位线知识得到线线平行,从而得到线面平行;
(2)建立适当的空间坐标系,设出P点坐标,求出直线PA与BC所对应的向量,利用两向量所成角为60°求正四棱锥的高,从而求出等腰三角形的腰长;
(3)求出相邻两个侧面的法向量,利用法向量所成角的余弦值求相邻两个侧面所成的二面角的余弦值.
(2)建立适当的空间坐标系,设出P点坐标,求出直线PA与BC所对应的向量,利用两向量所成角为60°求正四棱锥的高,从而求出等腰三角形的腰长;
(3)求出相邻两个侧面的法向量,利用法向量所成角的余弦值求相邻两个侧面所成的二面角的余弦值.
解答:(1)证明:如图,
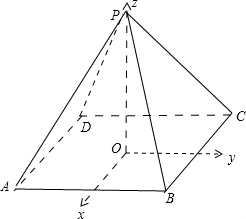
连结AC交BD于点O,连结OQ,∵点O,Q分别是AC,PC的中点,∴OQ∥AP,
又OQ?平面BDQ,PA?平面BDQ,∴PA∥平面BDQ;
(2)建立空间直角坐标系O-xyz如图所示,
不妨设高OP=x,则A(1,-1,0),P(0,0,x),
所以
=(-1,1,x),
=(-2,0,0).
所以cos<
,
>=
=
=
.
要使异面直线AP与BC所成的角为60°,只需
=cos60°=
,解得x=
.
此时侧棱长也就是三角形的腰长为2;
(3)侧棱与底面所成的角也就是∠PBO=60°时,
=
,而OB=
,所以OP=
所以
=(-1,1,
),
=(0,2,0).
不妨设平面PAB的一个法向量为
=(x,y,z),则有
,即
,令x=
,得y=0,z=1.
所以
=(
,0,1).
同理可得平面PBC的一个法向量为
=(0,
,1).
所以cos<
,
>=
=
=
.
所以相邻两个侧面所成二面角的余弦值为-
.

连结AC交BD于点O,连结OQ,∵点O,Q分别是AC,PC的中点,∴OQ∥AP,
又OQ?平面BDQ,PA?平面BDQ,∴PA∥平面BDQ;
(2)建立空间直角坐标系O-xyz如图所示,
不妨设高OP=x,则A(1,-1,0),P(0,0,x),
所以
| AP |
| BC |
所以cos<
| AP |
| BC |
| ||||
|
|
| 2 | ||
|
| 1 | ||
|
要使异面直线AP与BC所成的角为60°,只需
| 1 | ||
|
| 1 |
| 2 |
| 2 |
此时侧棱长也就是三角形的腰长为2;
(3)侧棱与底面所成的角也就是∠PBO=60°时,
| OP |
| OB |
| 3 |
| 2 |
| 6 |
所以
| AP |
| 6 |
| AB |
不妨设平面PAB的一个法向量为
| m |
|
|
| 6 |
所以
| m |
| 6 |
同理可得平面PBC的一个法向量为
| n |
| 6 |
所以cos<
| m |
| n |
| ||||
|
|
| 1 | ||||
|
| 1 |
| 7 |
所以相邻两个侧面所成二面角的余弦值为-
| 1 |
| 7 |
点评:本题考查了直线与平面平行的判定,考查了直线与平面所成的角,考查了二面角的平面角,利用空间向量求解线面角和二面角时,关键是选择适当的空间右手系,同时需要注意的是二面角与其平面法向量所成角的关系,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= 8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:
8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论: 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE. (2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
(2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为