题目内容
 (2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
(2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
| ||
| 4 |
| ||
| 4 |
分析:由题意得,CD⊥AD,CD⊥DE.可得正方形ABCD所在平面与正方形CDEF的二面角即∠CBE=60°,同时也得CD⊥平面ADE,进而求出CE、BE、BC,即可求出异面直线EC与直线AD所成的角的余弦值.
解答: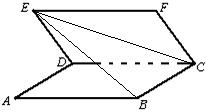 解:由题意得,CD⊥AD,CD⊥DE.可得正方形ABCD与正方形CDEF的二面角即∠ADE=60°,
解:由题意得,CD⊥AD,CD⊥DE.可得正方形ABCD与正方形CDEF的二面角即∠ADE=60°,
同时也得CD⊥平面ADE,
即三角形ADE为直角三角形和三角形CBF为等边三角形;
即是AB⊥BF.
设AB=1,则CE=
,BE=
,BC=1,
利用余弦定理,得 COS∠BCE=
.
则直线EC与直线AD所成的角的余弦值为
.
故答案为:
.
 解:由题意得,CD⊥AD,CD⊥DE.可得正方形ABCD与正方形CDEF的二面角即∠ADE=60°,
解:由题意得,CD⊥AD,CD⊥DE.可得正方形ABCD与正方形CDEF的二面角即∠ADE=60°,同时也得CD⊥平面ADE,
即三角形ADE为直角三角形和三角形CBF为等边三角形;
即是AB⊥BF.
设AB=1,则CE=
| 2 |
| 2 |
利用余弦定理,得 COS∠BCE=
| ||
| 4 |
则直线EC与直线AD所成的角的余弦值为
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:此题主要考查异面直线的角度及余弦定理,考查计算能力,属于基础题.

练习册系列答案
相关题目
 (2010•温州二模)设AD是半径为5的半圆O的直径(如图),B,C是半圆上两点,已知
(2010•温州二模)设AD是半径为5的半圆O的直径(如图),B,C是半圆上两点,已知