题目内容
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=| 2 |
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A-BE-D的大小.
分析:(Ⅰ)设AC与BD交于点G,则在平面BDE中,可以先证明四边形AGEF为平行四边形?EG∥AF,就可证:AF∥平面BDE;
(Ⅱ)先以C为原点,建立空间直角坐标系C-xyz.把对应各点坐标求出来,可以推出
•
=0和
•
=0,就可以得到CF⊥平面BDE
(Ⅲ)先利用(Ⅱ)找到
=(
,
,1),是平面BDE的一个法向量,再利用平面ABE的法向量
•
=0和
•
=0,求出平面ABE的法向量
,就可以求出二面角A-BE-D的大小.
(Ⅱ)先以C为原点,建立空间直角坐标系C-xyz.把对应各点坐标求出来,可以推出
| CF |
| BE |
| CF |
| DE |
(Ⅲ)先利用(Ⅱ)找到
| CF |
| ||
| 2 |
| ||
| 2 |
| n |
| BA |
| n |
| BE |
| n |
解答: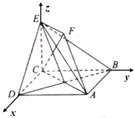 解:证明:(I)设AC与BD交于点G,
解:证明:(I)设AC与BD交于点G,
因为EF∥AG,且EF=1,AG=
AC=1,
所以四边形AGEF为平行四边形.所以AF∥EG.
因为EG?平面BDE,AF?平面BDE,
所以AF∥平面BDE.
(II)因为正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,
所以CE⊥平面ABCD.
如图,以C为原点,建立空间直角坐标系C-xyz.
则C(0,0,0),A(
,
,0),D(
,0,0),E(0,0,1),F(
,
,1).
所以
=(
,
,1),
=(0,-
,1),
=(-
,0,1).
所以
•
=0-1+1=0,
•
=-1+0+1=0.
所以CF⊥BE,CF⊥DE,所以CF⊥平面BDE
(III)由(II)知,
=(
,
,1),是平面BDE的一个法向量,
设平面ABE的法向量
=(x,y,z),则
•
=0,
•
=0.
即
所以x=0,且z=
y.令y=1,则z=
.所以n=(0,1,
),从而cos(
,
)=
=
因为二面角A-BE-D为锐角,所以二面角A-BE-D为
.
 解:证明:(I)设AC与BD交于点G,
解:证明:(I)设AC与BD交于点G,因为EF∥AG,且EF=1,AG=
| 1 |
| 2 |
所以四边形AGEF为平行四边形.所以AF∥EG.
因为EG?平面BDE,AF?平面BDE,
所以AF∥平面BDE.
(II)因为正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,
所以CE⊥平面ABCD.
如图,以C为原点,建立空间直角坐标系C-xyz.
则C(0,0,0),A(
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
所以
| CF |
| ||
| 2 |
| ||
| 2 |
| BE |
| 2 |
| DE |
| 2 |
所以
| CF |
| BE |
| CF |
| DE |
所以CF⊥BE,CF⊥DE,所以CF⊥平面BDE
(III)由(II)知,
| CF |
| ||
| 2 |
| ||
| 2 |
设平面ABE的法向量
| n |
| n |
| BA |
| n |
| BE |
即
|
所以x=0,且z=
| 2 |
| 2 |
| 2 |
| n |
| CF |
| ||||
|
|
| ||
| 2 |
因为二面角A-BE-D为锐角,所以二面角A-BE-D为
| π |
| 6 |
点评:本题综合考查直线和平面垂直的判定和性质和线面平行的推导以及二面角的求法.在证明线面平行时,其常用方法是在平面内找已知直线平行的直线.当然也可以用面面平行来推导线面平行.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:
8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论: 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE. (2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
(2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为