题目内容
已知二次函数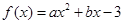 在
在 处取得极值,且在
处取得极值,且在 点处的切线与直线
点处的切线与直线 平行。
平行。
(1)求 的解析式;
的解析式;
(2)求函数 的单调递增区间及极值;
的单调递增区间及极值;
(3)求函数 在
在 的最值。
的最值。
【答案】
(1) 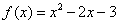 .
.
(2)增区间为 ,
,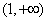 .在
.在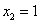 有极小值为0。在
有极小值为0。在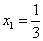 有极大值4/27。
有极大值4/27。
(3)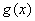 的最大值为2,最小值为0。
的最大值为2,最小值为0。
【解析】(1)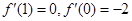 可建立关于a,b的方程解方程组即可求解。
可建立关于a,b的方程解方程组即可求解。
(2)先求出y=g(x)的解析式,然后再利用导数研究其单调区间及极值。
(3)在(2)的基础上,再求出g(0),g(2)然后与极值比较,最大的那个就是g(x)的最大值,最小的就是g(x)的最小值。
解:(1)由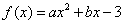 ,可得
,可得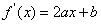 .
.
由题设可得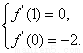 即
即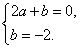
解得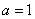 ,
,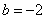 .所以
.所以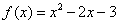 .
----------------------------4
.
----------------------------4
(2)由题意得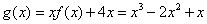 ,
,
所以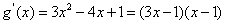 .令
.令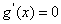 ,得
,得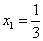 ,
,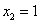 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4/27 |
|
0 |
|
所以函数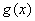 的单调递增区间为
的单调递增区间为 ,
,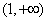 .在
.在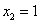 有极小值为0。在
有极小值为0。在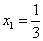 有极大值4/27。
有极大值4/27。
(3)由 及(2),所以函数
及(2),所以函数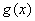 的最大值为2,最小值为0。
的最大值为2,最小值为0。

练习册系列答案
相关题目
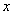

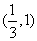
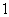
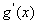
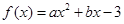 在
在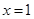 处取得极值,且在
处取得极值,且在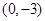 点处的切线与直线
点处的切线与直线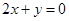 平行.
平行. 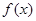 的解析式; (2)求函数
的解析式; (2)求函数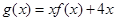 的单调递增区间及极值;
的单调递增区间及极值;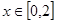 的最值.
的最值.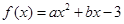 在
在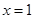 处取得极值,且在
处取得极值,且在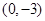 点处的切线与直线
点处的切线与直线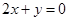 平行.
平行.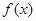 的解析式;
的解析式;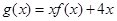 的单调递增区间与极值.
的单调递增区间与极值.