题目内容
已知二次函数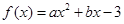 在
在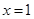 处取得极值,且在
处取得极值,且在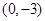 点处的切线与直线
点处的切线与直线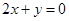 平行.
平行.
(1)求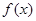 的解析式; (2)求函数
的解析式; (2)求函数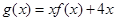 的单调递增区间及极值;
的单调递增区间及极值;
(3)求函数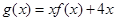 在
在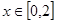 的最值.
的最值.
【答案】
解: (1) 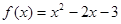 .
.
(2) 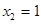 有极小值为0. 在
有极小值为0. 在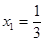 有极大值
有极大值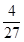 .
.
(3)由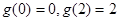 及(2),得,函数
及(2),得,函数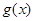 的最大值为2,最小值为0.
的最大值为2,最小值为0.
【解析】本题考查导数在求闭区间上函数最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答
(1)由f(x)=ax2+bx-3,知f′(x)=2ax+b.由二次函数f(x)=ax2+bx-3在x=1处取得极值,且在(0,-3)点处的切线与直线2x+y=0平行,知 f′(1)=2a+b=0,f′(0)=b=-2
,由此能求出f(x).(2)由f(x)=x2-2x-3,知g(x)=xf(x)+4x=x3-2x2+x,所以g′(x)=3x2-4x+1=(3x-1)(x-1).令g′(x)=0,得x1=
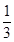 ,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.
,x2=1.列表讨论能求出函数g(x)=xf(x)+4x的单调递增区间及极值.
(3)由g(0)=0,g(2)=2,结合(2)的结论,能求出函数g(x)的最大值和最小值.

练习册系列答案
相关题目
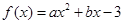 在
在 处取得极值,且在
处取得极值,且在 点处的切线与直线
点处的切线与直线 平行。
平行。  的解析式;
的解析式;  的单调递增区间及极值;
的单调递增区间及极值; 的最值。
的最值。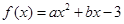 在
在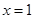 处取得极值,且在
处取得极值,且在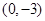 点处的切线与直线
点处的切线与直线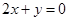 平行.
平行.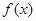 的解析式;
的解析式;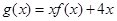 的单调递增区间与极值.
的单调递增区间与极值.