题目内容
如图,长方体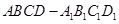 中,
中,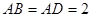 ,
,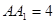 ,点
,点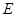 在
在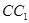 上,且
上,且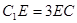 .
.

(Ⅰ)证明: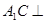 平面
平面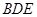 ;
;
(Ⅱ)求二面角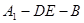 的余弦值.
的余弦值.
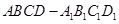 中,
中,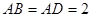 ,
,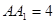 ,点
,点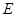 在
在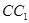 上,且
上,且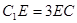 .
.
(Ⅰ)证明:
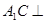 平面
平面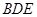 ;
;(Ⅱ)求二面角
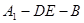 的余弦值.
的余弦值.(Ⅰ)建立空间直角坐标系,利用空间向量解决(Ⅱ)

试题分析:(Ⅰ)以
 为坐标原点,分别以
为坐标原点,分别以 、
、 、
、 所在的直线为
所在的直线为 轴、
轴、 轴、
轴、 轴,建立如下图所示的空间直角坐标系
轴,建立如下图所示的空间直角坐标系 .则
.则 .
. ,
, . ……2分
. ……2分有
 ,
, ,
,故
 ,
, .
.又
 ,所以
,所以 平面
平面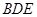 . ……6分
. ……6分(Ⅱ)由(Ⅰ)得
 是平面
是平面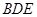 的一个法向量,
的一个法向量,设向量
 是平面
是平面 的法向量,则
的法向量,则

令
 ,则
,则 ,
, ,
, . ……10分
. ……10分
 .
.所以二面角
 的余弦值为
的余弦值为 . ……13分
. ……13分
点评:用空间向量证明立体几何问题的依据还是相应的判定定理,如第一问中必须强调
 ;另外,用法向量求二面角时,求出的可能是要求的角的补角,要仔细判断二面角时锐角还是钝角.
;另外,用法向量求二面角时,求出的可能是要求的角的补角,要仔细判断二面角时锐角还是钝角.
练习册系列答案
相关题目
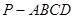 中,四边形
中,四边形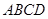 为正方形,
为正方形,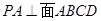 ,且
,且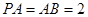 ,
,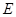 为
为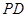 中点.
中点.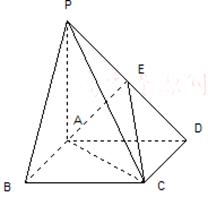
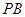 //平面
//平面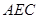 ;
;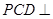 平面
平面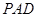 ;
;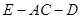 的正弦值.
的正弦值. 的中心,则直线EF与平面ABC所成的角的正切值是 。
的中心,则直线EF与平面ABC所成的角的正切值是 。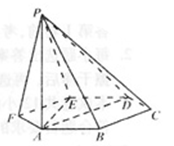
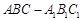 中,
中,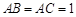 ,
,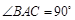 ,且异面直线
,且异面直线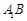 与
与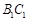 所成的角等于
所成的角等于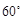 .
.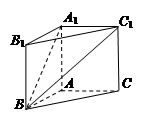
 所成的角的大小.
所成的角的大小. 中,
中, ,
, ,
, 为
为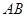 中点,
中点,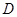 为
为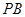 中点,且
中点,且 为正三角形.
为正三角形.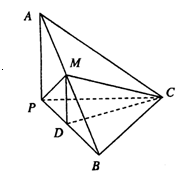
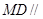 平面
平面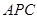 .
.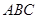 ⊥平面
⊥平面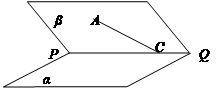
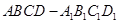 是正方体,其中
是正方体,其中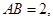

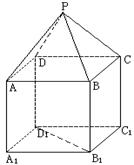
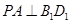 ;
;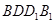 所成的锐二面角
所成的锐二面角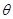 的余弦值;
的余弦值;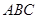 为底面的直棱柱被平面
为底面的直棱柱被平面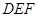 所截而得.
所截而得. 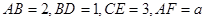 ,
, 为
为 的中点.
的中点.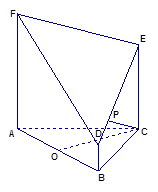
 时,求平面
时,求平面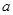 为何值时,在棱
为何值时,在棱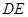 上存在点
上存在点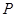 ,使
,使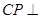 平面
平面