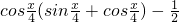Question

设函数y=f（x）满足：对任意x∈R都有f（x）＞0，且f（x+y）=f（x）•f（y）（x，y∈R）
（1）求f（0）的值；
（2）求f（x）•f（-x）的值；
（3）判断函数g（x）=

1+f(x)

1-f(x)

是否具有奇偶性，并证明你的结论．

Answer 1

分析：（1）令x=y=0可得f（0）；（2）令y=0可得；（3）由奇偶性定义证明．

解答：解：（1）令x=y=0得f（0）=1；
（2）令y=0得：f（x）f（-x）=1；
（3）由函数g（x）=

1+f(x)

1-f(x)

得：
g（-x）=

1+f(-x)

1-f(-x)

由（2）知f（x）f（-x）=1，
∴g（-x）=-g（x）
∴g（x）是奇函数．

点评：本题主要考查抽象函数中赋值法求值、研究奇偶性等问题，要注意变形处理和函数单调性奇偶性定义的应用