��Ŀ����
����Ŀ��Ϊ�˽�ѧ���Ŀ����Ķ�ʱ�������ijѧУ�����ȡ�� 50�˽���ͳ�Ʒ���������50��ÿ���Ķ���ʱ��(��λ:����)���Ƴ�Ƶ���ֲ��������±���ʾ��

����ÿ���Ķ�ʱ����60�������ϣ���60���ӣ���ͬѧ��Ϊ���Ķ����ˡ�������ͳ�ƽ������Ů���Ķ����˵����ݣ���������ͼ��ʾ�ĵȸ�����ͼ.
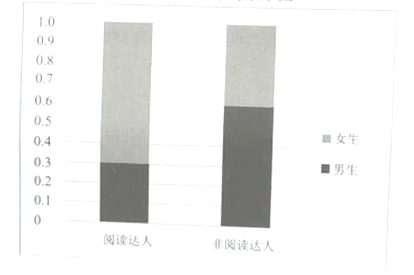
��1�����ݳ���������Ƹ�Уѧ����ÿ��ƽ���Ķ�ʱ�䣨ͬһ�������ø�������е�ֵ��Ϊ��������
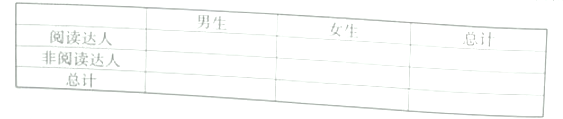
��2��������֪������������![]() �����������ж��Ƿ���
�����������ж��Ƿ���![]() �İ�����Ϊ���Ķ����ˡ����Ա��йأ�
�İ�����Ϊ���Ķ����ˡ����Ա��йأ�
�����ο���ʽ
![]() ������
������![]() .
.
�ٽ�ֵ����
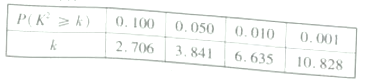
���𰸡���1��![]() ����2��û��
����2��û��![]() �İ�����Ϊ���Ķ����ˡ����Ա��й�.
�İ�����Ϊ���Ķ����ˡ����Ա��й�.
�������������������1�����ø���������е�ֵ��Ƶ�ʣ����ɹ��Ƹ�Уѧ����ÿ��ƽ���Ķ�ʱ������2���������ݼ��ȸ�����ͼ���ɵ�![]() �����������빫ʽ�����
�����������빫ʽ�����![]() �����ٽ�ֵ�Ƚϼ��ɵõ�����.
�����ٽ�ֵ�Ƚϼ��ɵõ�����.
�����������1����Уѧ����ÿ��ƽ���Ķ�ʱ��Ϊ�� ���֣�.
���֣�.
��2����Ƶ���ֲ����ã����Ķ���������������![]() �ˣ�
�ˣ�
���ݵȸ�����ͼ![]() ������
������

![]()
����![]() ����û��
����û��![]() �İ�����Ϊ���Ķ����������Ա��й�.
�İ�����Ϊ���Ķ����������Ա��й�.

����Ŀ��ij��ͨ���г�����õ���������ֲ�ɱ�![]() ����λ��Ԫ/ǧ�ˣ�������ʱ��
����λ��Ԫ/ǧ�ˣ�������ʱ��![]() ����λ��
����λ��![]() �죩���������±���
�죩���������±���
ʱ�� |
|
|
|
��ֲ�ɱ� |
|
|
|
��1�������ϱ����ݣ����ֶ��κ����ܹ��Ƚ�ȷ����![]() ��
��![]() �ı仯��ϵ������������Ľ���ʽ��
�ı仯��ϵ������������Ľ���ʽ��
��2������ѡȡ�ĺ������������������ֲ�ɱ�����ʱ����������.


