题目内容
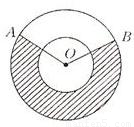
 如图所示,在同心圆中,两圆的半径分别为2,1,∠AOB=120°,则阴影部分的面积是( )
如图所示,在同心圆中,两圆的半径分别为2,1,∠AOB=120°,则阴影部分的面积是( )分析:阴影部分的形状是一个扇环,可以用大圆中圆心角为240度的扇形面积,减去小圆中圆心角为240度的扇形面积,得到这个扇环的面积.
解答:解:∵大圆的半径为2,优弧的圆心角为360°-120°=240°
∴大圆中的优弧对应的扇形面积为S1=
π•22 =
π
同理可得:小圆中的优弧对应的扇形面积为S2=
π•12 =
π
∴阴影部分的面积是S=S1-S2=2π
故选B
∴大圆中的优弧对应的扇形面积为S1=
| 240 |
| 360 |
| 8 |
| 3 |
同理可得:小圆中的优弧对应的扇形面积为S2=
| 240 |
| 360 |
| 2 |
| 3 |
∴阴影部分的面积是S=S1-S2=2π
故选B
点评:本题考查了用扇形的面积公式来求组合图形的面积的知识点,属于基础题.求扇环的面积时,常常化成两个扇形的面积之差,是一种常用的求法.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目