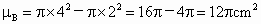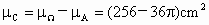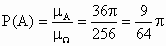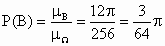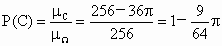题目内容
如图所示,在墙上挂着一块边长为16cm的正方形木板,上面画了小、中、大三个同心圆,半径分别为2cm,4cm,6cm,某人站在3m之外向此板投镖.设投镖击中线上或没有投中木板时都不算,可重投,问:

(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?
答案:略
解析:
解析:
|
解:整个正方形木板的面积,即基本事件所占的区域总面积为 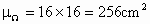 . .
记“投中大圆内”为事件 A,“投中小圆与中圆形成的圆环”为事件B,“投中大圆之外”为事件C,则事件 A所占区域面积为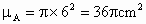 ; ;
事件 B所占区域面积为
事件 C所占区域面积为
由几何概型的概率公式,得 (1) (2) (3) 答:投中大圆内的概率是 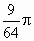 ;投中小圆与中圆形成的圆环的概率是 ;投中小圆与中圆形成的圆环的概率是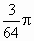 ;投中大圆之外的概率是 ;投中大圆之外的概率是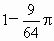 . .
对于 (3)的求解,也可以直接应用对立事件的性质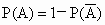 求解. 求解. |

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目