题目内容
对一切正整数n,不等式
<
恒成立,则b的范围是( )
| b |
| 1-b |
| n+1 |
| n+2 |
分析:将条件关系式
<
转化为
<
,对b-1的正负分类讨论结合题意即可解决.
| b |
| 1-b |
| n+1 |
| n+2 |
| 1 |
| n+2 |
| 2b-1 |
| b-1 |
解答:解:∴对一切正整数n,
<
=1-
恒成立,
∴
<1-
=
,
∴①若b-1>0,即b>1时,2b-1>0,
∴n+2>
恒成立,又n∈N*,
∴
<n+2<3,
∴b-1<6b-3,
∴b>
,又b>1,
∴b>1;
②若b-1<0,即b<1时,由题意得2b-1<0,
∴
<1-
=
恒成立?
<
恒成立?n+2>
恒成立,
同理可得,
<3,即1-b<3-6b,解得b<
,而b<1,
∴b<
.
综上所述,b的范围是(-∞,
)∪(1,+∞).
故选C.
| b |
| 1-b |
| n+1 |
| n+2 |
| 1 |
| n+2 |
∴
| 1 |
| n+2 |
| b |
| 1-b |
| 2b-1 |
| b-1 |
∴①若b-1>0,即b>1时,2b-1>0,
∴n+2>
| b-1 |
| 2b-1 |
∴
| b-1 |
| 2b-1 |
∴b-1<6b-3,
∴b>
| 2 |
| 5 |
∴b>1;
②若b-1<0,即b<1时,由题意得2b-1<0,
∴
| 1 |
| n+2 |
| b |
| 1-b |
| 2b-1 |
| b-1 |
| 1 |
| n+2 |
| 1-2b |
| 1-b |
| 1-b |
| 1-2b |
同理可得,
| 1-b |
| 1-2b |
| 2 |
| 5 |
∴b<
| 2 |
| 5 |
综上所述,b的范围是(-∞,
| 2 |
| 5 |
故选C.
点评:本题考查恒成立问题,着重考查转化与分类讨论思想的综合运用,考查解不等式组的能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
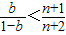 恒成立,则B的范围是 .
恒成立,则B的范围是 .