题目内容
对一切正整数n,不等式bn+2b<n+1恒成立,则b的范围是
(-∞,
)
| 2 |
| 3 |
(-∞,
)
.| 2 |
| 3 |
分析:由不等式bn+2b<n+1对一切正整数n恒成立可得b<
对一切正整数n恒成立,令f(n)=
,则由数列的单调性可得f(n+1)>f(n)>f(n-1)>…f(1)=
,从而可得b<f(1)可求
| n+1 |
| n+2 |
| n+1 |
| n+2 |
| 2 |
| 3 |
解答:解:因为不等式bn+2b<n+1对一切正整数n恒成立,
所以,b<
对一切正整数n恒成立,
令f(n)=
,则f(n+1)-f(n+1)=
-
=
>0;
∴f(n+1)>f(n)>f(n-1)>…f(1)=
,
∴b<
故答案为:(-∞,
)
所以,b<
| n+1 |
| n+2 |
令f(n)=
| n+1 |
| n+2 |
| n+2 |
| n+3 |
| n+1 |
| n+2 |
| 1 |
| (n+2)(n+3) |
∴f(n+1)>f(n)>f(n-1)>…f(1)=
| 2 |
| 3 |
∴b<
| 2 |
| 3 |
故答案为:(-∞,
| 2 |
| 3 |
点评:本题主要考查了恒成立问题与最值的相互转化,要注意数列单调性在解题中的应用.

练习册系列答案
相关题目
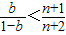 恒成立,则B的范围是 .
恒成立,则B的范围是 .