题目内容
(本题满分12分)
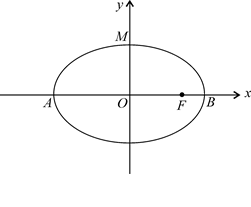
如图,椭圆长轴端点为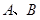 ,
,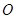 为椭圆中心,
为椭圆中心,
 为椭圆的右焦点,
为椭圆的右焦点,
且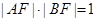 ,
,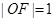 .
.
(1)求椭圆的标准方程;
(2)记椭圆的上顶点为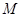 ,直线
,直线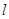 交椭圆于
交椭圆于 两点,问:是否存在直线
两点,问:是否存在直线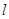 ,使点
,使点 恰为
恰为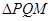 的垂心?若存在,求出直线
的垂心?若存在,求出直线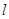 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(1)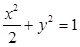 ; (2)3x-3y-4=0
; (2)3x-3y-4=0
解析试题分析:(1)设椭圆方程为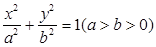 ,则
,则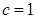
又∵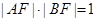 即
即 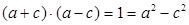 ,∴
,∴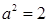
故椭圆方程为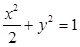
(2)假设存在直线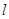 交椭圆于
交椭圆于 两点,且
两点,且 恰为
恰为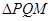 的垂心,则
的垂心,则
设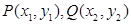 ,∵
,∵ ,故
,故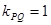 ,
,
于是设直线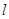 为
为 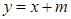 ,由
,由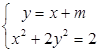 得
得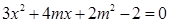
∵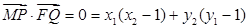 又
又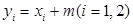
得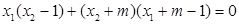 即
即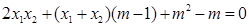 由韦达定理得
由韦达定理得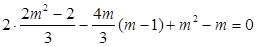
解得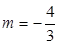 或
或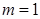 (舍) 经检验
(舍) 经检验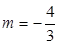 符合条件
符合条件
考点:本题考查了椭圆方程求法及直线与椭圆的位置关系
点评:椭圆的概念和性质,仍将是今后命题的热点,利用直线、弦长、圆锥曲线三者的关系组成的各类试题是解析几何中长盛不衰的主题,其中求解与相交弦有关的综合题仍是今后命题的重点;与其它知识的交汇(如向量、不等式)命题将是今后高考命题的一个新的重点、热点

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
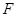 为抛物线
为抛物线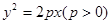 的焦点,点
的焦点,点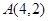 为抛物线内一定点,点
为抛物线内一定点,点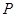 为抛物线上一动点,
为抛物线上一动点,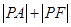 最小值为8.
最小值为8.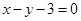 与抛物线交于
与抛物线交于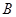 、
、 两点,求
两点,求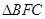 的面积.
的面积.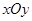 中,以O为极点,
中,以O为极点,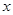 轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为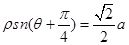 ,曲线
,曲线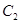 的参数方程为
的参数方程为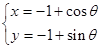 ,(
,(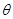 为参数,
为参数,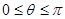 )。
)。 的取值范围。
的取值范围。 为抛物线
为抛物线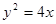 的焦点,
的焦点,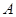 为抛物线上任意一点,已
为抛物线上任意一点,已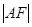 为半径画圆,与
为半径画圆,与 轴负半轴交于
轴负半轴交于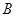 点,试判断过
点,试判断过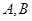 的直线与抛物线的位置关系,并证明。
的直线与抛物线的位置关系,并证明。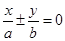 称为椭圆
称为椭圆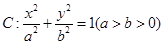 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率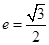 .(1)求椭圆的“特征直线”方程;
.(1)求椭圆的“特征直线”方程;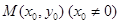 作圆
作圆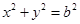 的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若
的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若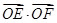 取值范围恰为
取值范围恰为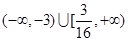 ,求椭圆C的方程.
,求椭圆C的方程.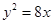 的焦点,M的离心率
的焦点,M的离心率 ,过M的右焦点F作不与坐标轴垂直的直线
,过M的右焦点F作不与坐标轴垂直的直线 ,交M于A,B两点。
,交M于A,B两点。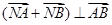 ,求实数t的取值范围。
,求实数t的取值范围。 中,已知三点
中,已知三点 ,
,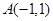 ,
, ,曲线C上任意—点
,曲线C上任意—点 满足:
满足: .
. ,
, .试探究
.试探究 的值是否与点P及直线L有关,并证明你的结论;
的值是否与点P及直线L有关,并证明你的结论; 取得最小值,求实数m的取值范围.
取得最小值,求实数m的取值范围.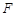 为抛物线
为抛物线 :
: 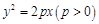 的焦点,
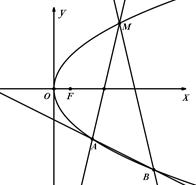
的焦点, 为抛物线
为抛物线 .
.
 的坐标;
的坐标;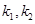 的两直线
的两直线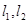 ,
, 与抛物线
与抛物线 ,
, 与抛物线
与抛物线 ,记直线
,记直线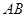 的斜率为
的斜率为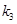 .
. ,试求
,试求 为定值.
为定值.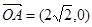 ,
,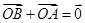 ,O为坐标原点,动点E满足:
,O为坐标原点,动点E满足: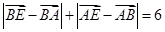
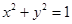 引两条切线PA、PB,切点分别为A、B,直线AB与x轴、y轴分别交于M、N两点,求ΔMON面积的最小值.
引两条切线PA、PB,切点分别为A、B,直线AB与x轴、y轴分别交于M、N两点,求ΔMON面积的最小值.