题目内容
(本小题满分12分,(Ⅰ)小问3分,(Ⅱ)小问9分.)
直线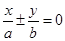 称为椭圆
称为椭圆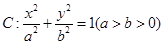 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率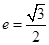 .(1)求椭圆的“特征直线”方程;
.(1)求椭圆的“特征直线”方程;
(2)过椭圆C上一点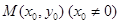 作圆
作圆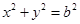 的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若
的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若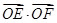 取值范围恰为
取值范围恰为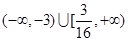 ,求椭圆C的方程.
,求椭圆C的方程.
(1)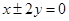 ;(2)
;(2) ;
;
解析试题分析:(1)设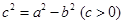 ,则由
,则由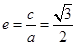 ,得
,得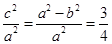 ,
,
椭圆的“特征直线”方程为: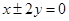 …………………………………………….3分
…………………………………………….3分
(2)直线PQ的方程为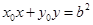 (过程略) ……………………………….5分
(过程略) ……………………………….5分
设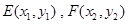
联立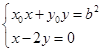 ,解得
,解得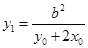 ,同理
,同理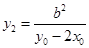 ……………….7分
……………….7分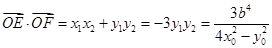 ,
,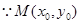 是椭圆上的点,
是椭圆上的点,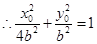
从而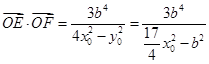 ……………………………………….10分
……………………………………….10分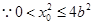

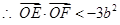 或
或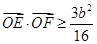
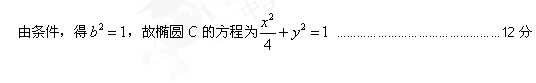
考点:椭圆的简单性质;直线与椭圆的综合应用。
点评:本题考查椭圆的简单性质,两个向量的数量积公式,以及不等式的性质的应用,较为综合。直线与椭圆的综合应用,在考试中经常考到,这种类型的题目,计算较为繁琐,我们在计算时要有耐心、又要细心。

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
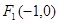 及
及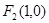 ,点
,点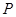 在以
在以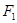 、
、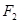 为焦点的椭圆
为焦点的椭圆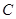 上,且
上,且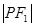 、
、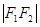 、
、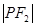 构成等差数列.
构成等差数列.
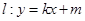 与椭圆
与椭圆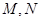 是直线
是直线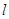 上的两点,且
上的两点,且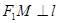 ,
,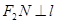 . 求四边形
. 求四边形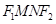 面积
面积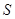 的最大值.
的最大值.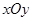 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为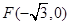 ,右顶点为
,右顶点为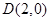 ,设点
,设点 .
.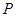 是椭圆上的动点,求线段
是椭圆上的动点,求线段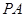 中点
中点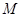 的轨迹方程;
的轨迹方程; 的直线交椭圆于点
的直线交椭圆于点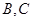 ,求
,求 面积的最大值。
面积的最大值。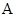 、
、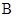 、
、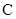 是椭圆
是椭圆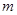 :
: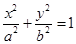 (
(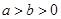 )上的三点,其中点
)上的三点,其中点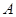 的坐标为
的坐标为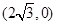 ,
,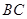 过椭圆的中心,且
过椭圆的中心,且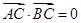 ,
, 。
。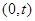 的直线
的直线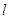 (斜率存在时)与椭圆
(斜率存在时)与椭圆 ,
,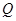 ,设
,设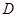 为椭圆
为椭圆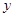 轴负半轴的交点,且
轴负半轴的交点,且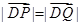 ,求实数
,求实数 的取值范围.
的取值范围.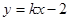 相交于不同的两点A、B,且AB中点横坐标为2,求k的值.
相交于不同的两点A、B,且AB中点横坐标为2,求k的值.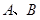 ,
,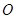 为椭圆中心,
为椭圆中心,
 为椭圆的右焦点,
为椭圆的右焦点,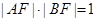 ,
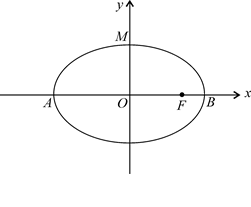
,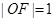 .
.
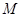 ,直线
,直线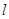 交椭圆于
交椭圆于 两点,问:是否存在直线
两点,问:是否存在直线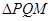 的垂心?若存在,求出直线
的垂心?若存在,求出直线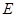 :
: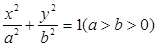 的右焦点
的右焦点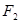 与抛物线
与抛物线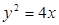 的焦点重合,过
的焦点重合,过 轴垂直的直线
轴垂直的直线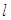 与椭圆交于
与椭圆交于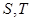 两点,与抛物线交于
两点,与抛物线交于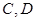 两点,且
两点,且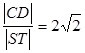 。
。 的直线与椭圆
的直线与椭圆 ,设
,设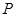 为椭圆
为椭圆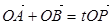
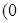 为坐标原点),当
为坐标原点),当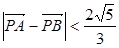 时,求实数
时,求实数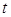 的取值范围。
的取值范围。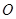 ,焦点在
,焦点在 轴上,两条渐近线分别为
轴上,两条渐近线分别为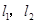 ,经过右焦点
,经过右焦点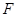 垂直于
垂直于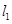 的直线分别交
的直线分别交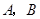 两点.已知
两点.已知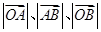 成等差数列,且
成等差数列,且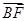 与
与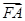 同向.
同向.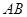 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.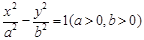 的渐近线,△P1OP2的面积为
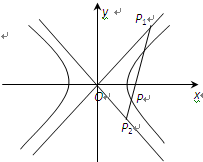
的渐近线,△P1OP2的面积为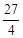 ,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为
,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为 .
.
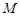 ,两焦点
,两焦点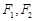 ,若
,若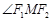 为钝角,求
为钝角,求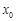 的取值范围.
的取值范围.