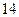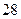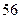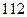题目内容
883+6被49除所得的余数是( )
| A.0 | B.14 | C.-14 | D.35 |
由二项式定理展开得883+6=(7+1)83+6
=783+
×782+…+
×72+
×7+1+6
=72M+83×7+7(M是正整数)
=49M+49×12
=49N.(N是正整数).
∴883+6被49除所得的余数是0.
故选A.
=783+
| C | 183 |
| C | 8183 |
| C | 8283 |
=72M+83×7+7(M是正整数)
=49M+49×12
=49N.(N是正整数).
∴883+6被49除所得的余数是0.
故选A.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
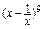 的展开式中第3项是
的展开式中第3项是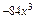
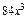
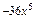

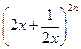 的展开式中,
的展开式中,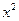 的系数是
的系数是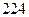 ,则
,则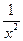 的系数是( )
的系数是( )