题目内容
在(x4+
)n的展开式中,第三项的二项式系数比第二项的二项式系数大35.
(1)求n的值;
(2)求展开式中的常数项.
| 1 |
| x |
(1)求n的值;
(2)求展开式中的常数项.
(1)∵第三项的二项式系数比第二项的二项式系数大35.
∴
-
=35,即
-n=35,
解得n=10或n=-7(舍掉).
(2)展开式的通项公式为Tr+1=
(x4)10-r•(
)r=
x40-5r,
由40-5r=0,解得r=8.
即展开式中的常数项为T9=
=45.
∴
| C | 2n |
| C | 1n |
| n(n-1) |
| 2 |
解得n=10或n=-7(舍掉).
(2)展开式的通项公式为Tr+1=
| C | r10 |
| 1 |
| x |
| C | r10 |
由40-5r=0,解得r=8.
即展开式中的常数项为T9=
| C | 810 |

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
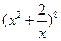 的展开式中
的展开式中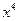 的系数是( )
的系数是( )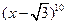 的展开式中,
的展开式中,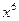 的系数是 .
的系数是 .