题目内容
(本小题满分12分)
已知集合A={x|log2(x-1)<1},集合B={x|x2-ax+b<0,a,b∈R}.
(1)若A=B,求a,b的值;
(2)若b=3,且A∪B=A,求a的取值范围.
【答案】
(1)a=4,b=3
(2)[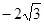 ,4]
,4]
【解析】解:(1)由log2(x-1)<1得0<x-1<2,所以集合A={x|1<x<3}。 (2')
由A=B知,x2-ax+b<0的解集为{x|1<x<3},所以方程x2-ax+b=0的两根分别为1和3。
由韦达定理可知,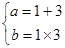 ,解得a=4,b=3,即为所求。
(4')
,解得a=4,b=3,即为所求。
(4')
(2)由A∪B=A知,B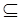 A。
(5')
A。
(5')
①当B=φ时,有Δ=a2-12≤0,解得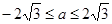 ;
(7')
;
(7')
②当B≠φ时,设函数f(x)=x2-ax+3,其图象的对称轴为x=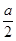 ,则
,则
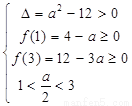 ,解之得
,解之得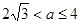 。
(11')
。
(11')
综上①②可知,实数a的取值范围是[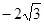 ,4]。
(12')
,4]。
(12')

练习册系列答案
相关题目