题目内容
(文科)设函数 ,其中a∈R,m是给定的正整数,且m≥2.如果不等式f(x)>(x-1)lgm在区间[1,+∞)上有解,则实数a的取值范围是________.
,其中a∈R,m是给定的正整数,且m≥2.如果不等式f(x)>(x-1)lgm在区间[1,+∞)上有解,则实数a的取值范围是________.
a>
分析:依据题意利用函数解析式,根据题设不等式求得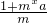 >mx-1.分离参数得
>mx-1.分离参数得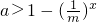 ,故求右边函数的最小值即可求得a范围.
,故求右边函数的最小值即可求得a范围.
解答: >(x-1)lgm=lgmx-1,
>(x-1)lgm=lgmx-1,
∴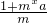 >mx-1.
>mx-1.
∴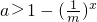
∵m≥2,∴g(x)=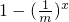 在[1,+∞)上单调递增.
在[1,+∞)上单调递增.
∴g(x)min=g(1)=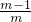
∴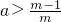 .
.
∵m≥2,∴a>
故答案为:a> .
.
点评:本题的考点是函数恒成立问题,主要考查了函数的单调性的性质.考查了学生对函数基础知识的掌握程度.考查分离参数法研究函数恒成立问题.

分析:依据题意利用函数解析式,根据题设不等式求得
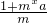 >mx-1.分离参数得
>mx-1.分离参数得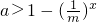 ,故求右边函数的最小值即可求得a范围.
,故求右边函数的最小值即可求得a范围.解答:
 >(x-1)lgm=lgmx-1,
>(x-1)lgm=lgmx-1,∴
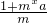 >mx-1.
>mx-1.∴
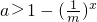
∵m≥2,∴g(x)=
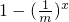 在[1,+∞)上单调递增.
在[1,+∞)上单调递增.∴g(x)min=g(1)=
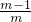
∴
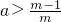 .
.∵m≥2,∴a>

故答案为:a>
 .
.点评:本题的考点是函数恒成立问题,主要考查了函数的单调性的性质.考查了学生对函数基础知识的掌握程度.考查分离参数法研究函数恒成立问题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 ·
· ,其中
,其中 ,2).
,2). 知函数f(x)=ex-kx,x∈R
知函数f(x)=ex-kx,x∈R ,其中a∈R,m是给定的正整数,且m≥2.如果不等式f(x)>(x-1)lgm在区间[1,+∞)上有解,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2.如果不等式f(x)>(x-1)lgm在区间[1,+∞)上有解,则实数a的取值范围是 .