题目内容
对于函数 ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数 为“可等域函数”,区间
为“可等域函数”,区间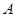 为函数
为函数 的一个“可等域区间”. 下列函数中存在唯一“可等域区间”的“可等域函数”为( )
的一个“可等域区间”. 下列函数中存在唯一“可等域区间”的“可等域函数”为( )
A. | B. |
C. | D.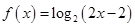 |
B
解析试题分析:根据题意,(A)中 与
与 都是
都是 的可等域区间,(B)中,
的可等域区间,(B)中, ,且
,且 在
在 时递减,在
时递减,在 时递增,若
时递增,若 ,则
,则 ,于是
,于是 ,又
,又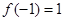 ,
, ,而
,而 ,故
,故 ,
, 是一个可等域区间,有没有可等域区间
是一个可等域区间,有没有可等域区间 ,且
,且 呢?若
呢?若 ,则
,则 ,解得
,解得 ,不合题意,若
,不合题意,若 ,则
,则 有两个非负解,但此方程的两解为1和
有两个非负解,但此方程的两解为1和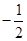 ,也不合题意,故函数
,也不合题意,故函数 只有一个可等域区间
只有一个可等域区间 ,应该选B,(C)中函数
,应该选B,(C)中函数 的值域是
的值域是 ,所以
,所以 ,函数
,函数 在R上是增函数,考察方程
在R上是增函数,考察方程 ,由于函数
,由于函数 与
与 没有交点,即方程
没有交点,即方程 无解,因此此函数没有可等域区间,对于(D),函数
无解,因此此函数没有可等域区间,对于(D),函数 在定义域
在定义域 上是增函数,若上函数有可等域区间
上是增函数,若上函数有可等域区间 ,则
,则 ,但方程
,但方程 无解(方程
无解(方程 无解),故此函数无可等域区间.综上只有(B)正确,选B.
无解),故此函数无可等域区间.综上只有(B)正确,选B.
考点:函数的定义域与值域,单调性,方程的解等综合问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用二分法求方程 的近似解,可以取的一个区间是( )
的近似解,可以取的一个区间是( )
A. | B. | C.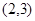 | D. |
已知函数 ,若关于
,若关于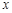 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数 则函数
则函数 的零点为( )
的零点为( )
A. 和1 和1 | B. 和0 和0 | C. | D. |
 ”,对任意
”,对任意 ,
, 为唯一确定的实数,且具有性质:
为唯一确定的实数,且具有性质: (2)对任意的
(2)对任意的 ,
, ;
;
 的性质,有如下说法:
的性质,有如下说法: ,其中所有正确说法的个数( )
,其中所有正确说法的个数( )
 的部分图像可能是( )
的部分图像可能是( )
 ,点
,点 在曲线
在曲线
 上,若线段
上,若线段 与曲线
与曲线
 相交且交点恰为线段
相交且交点恰为线段 关于曲线
关于曲线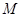 的一个关联点.记曲线
的一个关联点.记曲线 ,则( )
,则( )



 ,则
,则 的图象大致为( )
的图象大致为( )
 的棱长是1,点
的棱长是1,点 是对角线
是对角线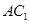 上一动点,记
上一动点,记 (
( ),过点
),过点 的截面将正方体分成两部分,其中点
的截面将正方体分成两部分,其中点 所在的部分的体积为
所在的部分的体积为 ,则函数
,则函数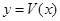 的图像大致为( )
的图像大致为( )



