题目内容
对于定义域为 的函数
的函数 ,如果同时满足以下三个条件:
,如果同时满足以下三个条件:
①对任意的 ,总有
,总有 ;②
;② ;③若
;③若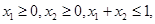 都有
都有 成立;
成立;
则称函数 为
为 函数.
函数.
下面有三个命题:
(1)若函数 为
为 函数,则
函数,则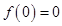 ;(2)函数
;(2)函数 是
是 函数;
函数;
(3)若函数 为
为 函数,假定存在
函数,假定存在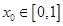 ,使得
,使得 ,且
,且 , 则
, 则 ; 其中真命题是________.(填上所有真命题的序号)
; 其中真命题是________.(填上所有真命题的序号)
(1)(2)(3).
解析试题分析:由①得 ,由③令
,由③令 ,得
,得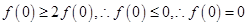 ,故(1)正确.若
,故(1)正确.若 ,函数
,函数 显然满足①②;对任意的满足条件
显然满足①②;对任意的满足条件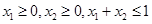 的
的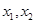 ,
,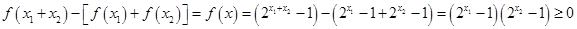 ,故③成立,所以(2)正确;对于(3),假设
,故③成立,所以(2)正确;对于(3),假设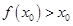 ,设
,设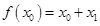 ,由③对任意的满足条件
,由③对任意的满足条件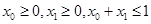 的
的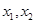 ,都有
,都有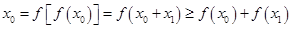 成立,从而
成立,从而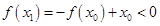 ,这与
,这与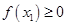 矛盾,同理可证,若假设
矛盾,同理可证,若假设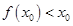 也推出矛盾,
也推出矛盾,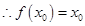 .
.
从而(3)也正确.
考点:1.新定义函数;2.函数的性质;3.反证法.

练习册系列答案
相关题目
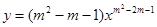 在
在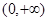 上是增函数,则
上是增函数,则 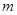 =_________.
=_________. .
. 是幂函数,且满足
是幂函数,且满足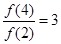 ,则
,则 的值等于 .
的值等于 .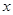 的不等式
的不等式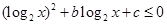 (
( 为实常数)的解集为
为实常数)的解集为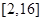 ,则关于
,则关于 的解集为 .
的解集为 .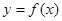 的图象上, 那么称[A, B]为函数f(x)的一组关于原点的中心对称点 ([A , B]与[B, A]看作一组). 函数
的图象上, 那么称[A, B]为函数f(x)的一组关于原点的中心对称点 ([A , B]与[B, A]看作一组). 函数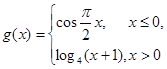 关于原点的中心对称点的组数为_____________
关于原点的中心对称点的组数为_____________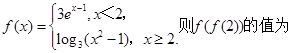 .
.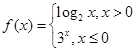 ,则
,则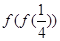 的值是 .
的值是 .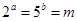 ,且
,且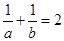 ,则
,则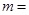 _________.
_________.