题目内容
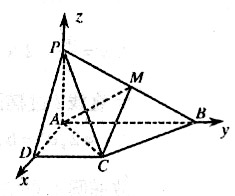
(08年德州市质检理)(12分) 已知四棱锥P―ABCD的底面为直角梯形,AB∥DC,∠DAB=900。,PA⊥底面ABCD且PA=AD=DC=1,AB=2,M是PB的中点
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求面AMC与面BMC所成二面角的大小

解析:以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为A(0,0,0),B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,1/2),
(1)因![]() =(0,0,1),
=(0,0,1),![]() =(0,1,0),
=(0,1,0),
故![]() ,所以AP⊥DC.
,所以AP⊥DC.
由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,
由此得DC⊥面PAD.
又DC在面PCD上,故面PAD⊥面PCD 4分
(2)因![]() =(1,1,0),
=(1,1,0),![]() =(0,2,-1),
=(0,2,-1),
故![]()
所以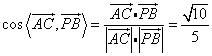
AC与PB所成的角为![]() 8分
8分
(3)由![]() =(0,1,1/2),
=(0,1,1/2),![]() =(1,0,一1/2),
=(1,0,一1/2),![]() =(一1,1,0)
=(一1,1,0)
设平面AMC与面BMC的法向量分别为![]() =(x,y,z),
=(x,y,z),![]() =(p,q,v),
=(p,q,v),
则![]() 解得:
解得:![]() =(1,一1,2),
=(1,一1,2),
同理![]() =(1,1,2),
=(1,1,2),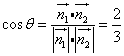
由题可知,二面角的平面角为钝角,
所以面AMC与面BMC二面角的大小![]() 12分
12分

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 时,求sin2A的值.
时,求sin2A的值.