题目内容
（08年德州市质检理） （12分） 设
为锐角，且
求
解析：由
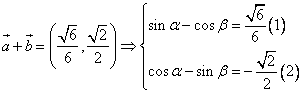
①2+②2
6分
又
为锐角
10分
12分
练习册系列答案
相关题目
时，求sin2A的值.
个红球，y个黄球，
个白球的箱子，且
（
、
），乙有一只放有3个红球，2个黄球，1个白球的箱子，两人各自从自己的箱子中任取一球，规定：当两球同色时甲胜，异色时乙胜
时，求
的单调区间；
，求出a的值