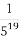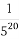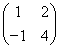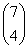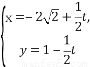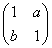题目内容
在平面直角坐标系xOy中,曲线C1的参数方程为 (φ为参数),曲线C2的参数方程为
(φ为参数),曲线C2的参数方程为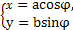 (a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=
(a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=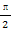 时,这两个交点重合.
时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值.
(2)设当α= 时,l与C1,C2的交点分别为A1,B1,当α=-
时,l与C1,C2的交点分别为A1,B1,当α=- 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
(1) C1是圆,C2是椭圆. a=3 b=1 (2) 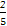
【解析】(1)C1是圆,C2是椭圆.
当α=0时,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0),因为这两点间的距离为2,a>0,所以a=3.当α= 时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),因为这两点重合,所以b=1.
时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),因为这两点重合,所以b=1.
(2) C1,C2的普通方程分别为x2+y2=1和 +y2=1.
+y2=1.
当α= 时,射线l与C1交点A1的横坐标为x=
时,射线l与C1交点A1的横坐标为x= ,与C2交点B1的横坐标为x'=
,与C2交点B1的横坐标为x'=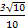 .
.
当α=- 时,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,因此,四边形A1A2B2B1为梯形.
时,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,因此,四边形A1A2B2B1为梯形.
故四边形A1A2B2B1的面积为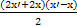 =
=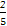 .
.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目