题目内容
过椭圆
+y2=1的左焦点F作斜率为k(k≠0)的直线交椭圆于A,B两点,使得AB的中点M在直线x+2y=0上.
(1)求k的值;
(2)设C(-2,0),求tan∠ACB.
| x2 | 2 |
(1)求k的值;
(2)设C(-2,0),求tan∠ACB.
分析:(1)由椭圆方程,a,b,c.直线AB方程为y=k(x+1),代入椭圆方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用中点坐标公式即可求得k值,从而解决问题.
(2)将k=1代入(1)中得到关于x的一元二次方程,求出方程的两个根,再根据夹角公式求出tan∠ACB.
(2)将k=1代入(1)中得到关于x的一元二次方程,求出方程的两个根,再根据夹角公式求出tan∠ACB.
解答:解:(1)由椭圆方程,a=
,b=1,c=1,则点F为(-1,0).
直线AB方程为y=k(x+1),代入椭圆方程,得
(2k2+1)x2+4k2x+2k2-2=0.①
设A(x1,y1),B(x2,y2),M(x0,y0),则
x0=
=-
,y0=k(x0+1)=
,
由点M在直线x+2y=0上,知-2k2+2k=0,
∵k≠0,
∴k=1.…(6分)
(2)将k=1代入①式,得3x2+4x=0,
不妨设x1>x2,则x1=0,x2=-
,…(8分)
记α=∠ACF,β=∠BCF,则
tanα=
=
=
,tanβ=-
=-
=
,
∴α=β,
∴tan∠ACB=tan2α=
=
.…(12分)
| 2 |
直线AB方程为y=k(x+1),代入椭圆方程,得
(2k2+1)x2+4k2x+2k2-2=0.①
设A(x1,y1),B(x2,y2),M(x0,y0),则
x0=
| x1+x2 |
| 2 |
| 2k2 |
| 2k2+1 |
| k |
| 2k2+1 |
由点M在直线x+2y=0上,知-2k2+2k=0,
∵k≠0,
∴k=1.…(6分)
(2)将k=1代入①式,得3x2+4x=0,
不妨设x1>x2,则x1=0,x2=-
| 4 |
| 3 |
记α=∠ACF,β=∠BCF,则
tanα=
| y1 |
| x1+2 |
| x1+1 |
| x1+2 |
| 1 |
| 2 |
| y2 |
| x2+2 |
| x2+1 |
| x2+2 |
| 1 |
| 2 |
∴α=β,
∴tan∠ACB=tan2α=
| 2tanα |
| 1-tan2α |
| 4 |
| 3 |
点评:本小题主要考查椭圆的简单性质、夹角公式等基础知识,考查运算求解能力,考查方程思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
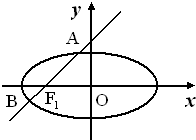 过椭圆
过椭圆