题目内容
已知极坐标系的极点在直角坐标系的原点O处,极轴与x轴的正半轴重合,直线l的参数方程为 (t为参数,α为直线l的倾斜角),圆C的极坐标方程为ρ2-8ρcosθ+12=0.若直线l与圆有公共点,则倾斜角α的范围为 .
(t为参数,α为直线l的倾斜角),圆C的极坐标方程为ρ2-8ρcosθ+12=0.若直线l与圆有公共点,则倾斜角α的范围为 .
【答案】分析:把直线的参数方程化为普通方程,把圆的极坐标方程化为直角坐标方程,根据圆心到直线的距离小于或等于半径,求得
sinα≤ ,由此求出倾斜角α的范围.
,由此求出倾斜角α的范围.
解答:解:∵直线l的参数方程为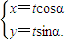 (t为参数,α为直线l的倾斜角),
(t为参数,α为直线l的倾斜角),
消去参数t化为普通方程为 tanα•x-y=0.
圆的极坐标方程为ρ2-8ρcosθ+12=0,化为直角坐标方程为 x2+y2-8x+12=0,即(x-4)2+y2=4,
表示以C(4,0)为圆心,以2为半径的圆.
根据圆心C到直线的距离d= =
= =4|tanα|•cosα|=4sinα≤2,解得sinα≤
=4|tanα|•cosα|=4sinα≤2,解得sinα≤ .
.
再由倾斜角α∈[0,π) 可得,0≤α≤ 或
或  ≤α<π.
≤α<π.
故倾斜角α的范围为[0, ]∪[
]∪[ ,π),
,π),
故答案为[0, ]∪[
]∪[ ,π).
,π).
点评:本题主要考查把参数方程化为普通方程,把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,根据三角函数的值求角,属于中档题.
sinα≤
 ,由此求出倾斜角α的范围.
,由此求出倾斜角α的范围.解答:解:∵直线l的参数方程为
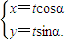 (t为参数,α为直线l的倾斜角),
(t为参数,α为直线l的倾斜角),消去参数t化为普通方程为 tanα•x-y=0.
圆的极坐标方程为ρ2-8ρcosθ+12=0,化为直角坐标方程为 x2+y2-8x+12=0,即(x-4)2+y2=4,
表示以C(4,0)为圆心,以2为半径的圆.
根据圆心C到直线的距离d=
 =
= =4|tanα|•cosα|=4sinα≤2,解得sinα≤
=4|tanα|•cosα|=4sinα≤2,解得sinα≤ .
.再由倾斜角α∈[0,π) 可得,0≤α≤
 或
或  ≤α<π.
≤α<π.故倾斜角α的范围为[0,
 ]∪[
]∪[ ,π),
,π),故答案为[0,
 ]∪[
]∪[ ,π).
,π).点评:本题主要考查把参数方程化为普通方程,把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,根据三角函数的值求角,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.