题目内容
已知等比数列{xn}的各项为不等于1的正数,数列{yn}满足
=2(a>0,且a≠1),设y3=18,y6=12.
(1)数列{yn}的前多少项和最大,最大值是多少?
(2)试判断是否存在自然数M,使得n>M时,xn>1恒成立,若存在,求出最小的自然数M,若不存在,请说明理由.
| yn |
| logaxn |
(1)数列{yn}的前多少项和最大,最大值是多少?
(2)试判断是否存在自然数M,使得n>M时,xn>1恒成立,若存在,求出最小的自然数M,若不存在,请说明理由.
(1)∵数列{yn}满足
=2(a>0,且a≠1),
∴yn=2logaxn,yn+1=2logaxn+1,
则yn+1-yn=2(logaxn+1-logaxn)=2loga(
).
∵{xn}为等比数列,
∴
为定值.
∴{yn}为等差数列.
∵y3=18,y6=12,
∴y6-y3=3d=12-18,
∴d=-2,y1=y3-2d=22.
∴Sn=22n+
•(-2)=-n2+23n.
∴当n=11或n=12时,Sn取得最大值,且最大值为132.
(2)∵yn=22+(n-1)(-2)=2logaxn,
∴xn=a12-n.又xn=a12-n>1,
当a>1时,12-n>0,n<12;
当0<a<1时,12-n<0,n>12.
综上所述,当0<a<1时,存在最小的自然数M=12,使得当n>M时,xn>1恒成立.
| yn |
| logaxn |
∴yn=2logaxn,yn+1=2logaxn+1,
则yn+1-yn=2(logaxn+1-logaxn)=2loga(
| xn+1 |
| xn |
∵{xn}为等比数列,
∴
| xn+1 |
| xn |
∴{yn}为等差数列.
∵y3=18,y6=12,
∴y6-y3=3d=12-18,
∴d=-2,y1=y3-2d=22.
∴Sn=22n+
| n(n-1) |
| 2 |
∴当n=11或n=12时,Sn取得最大值,且最大值为132.
(2)∵yn=22+(n-1)(-2)=2logaxn,
∴xn=a12-n.又xn=a12-n>1,
当a>1时,12-n>0,n<12;
当0<a<1时,12-n<0,n>12.
综上所述,当0<a<1时,存在最小的自然数M=12,使得当n>M时,xn>1恒成立.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
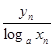 =2(a>0,且a≠1),设y3=18, y6=12.
=2(a>0,且a≠1),设y3=18, y6=12.
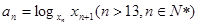 试比较
试比较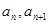 的大小.
的大小.